За последние годы технологии искусственного интеллекта и машинного обучения резко возросли в популярности, а с ними и требования к вычислительным ресурсам. Одной из центральных задач в этой области является эффективное умножение больших матриц, которое лежит в основе многих алгоритмов. Компания NVIDIA постоянно совершенствует архитектуру своих графических процессоров, внедряя специализированные ускорители, такие как Tensor Core, которые позволяют значительно увеличить производительность операций матричного умножения с плавающей запятой. В данном материале мы рассмотрим процесс создания высокопроизводительного ядра матричного умножения (matmul) с использованием Tensor Core на архитектуре Ada, которая легла в основу современных GPU NVIDIA RTX 4090 и подобных моделей. Tensor Core требуют понимания низкоуровневых инструкций PTX, таких как mma, ldmatrix и cp.
async. Работа с этими командами позволяет эффективно загружать данные в регистры GPU и организовывать вычисления с минимальными задержками и коллизиями при доступе к памяти. Архитектура Ada характеризуется наличием четырех warp scheduler'ов на одном Streaming Multiprocessor (SM), каждый из которых управляет собственным Tensor Core, что обуславливает архитектурные особенности составления и планирования вычислительных потоков. Начальных этапом стало создание наивного ядра умножения матриц с использованием инструкции mma.sync.
aligned.m16n8k16.row.col.f32.
f16.f16.f32. Эта команда позволяет перемножать подматрицы размером 16x16 и 16x8 с использованием половинной точности (fp16) для входных данных и одинарной точности (fp32) для накопления результата, что обеспечивает баланс между производительностью и точностью вычислений. Однако изначальная реализация оказалась крайне неэффективной из-за некоалесцированных загрузок из глобальной памяти и конфликтов банков при доступе к разделяемой памяти, что приводило к частым простоям и высокой латентности.
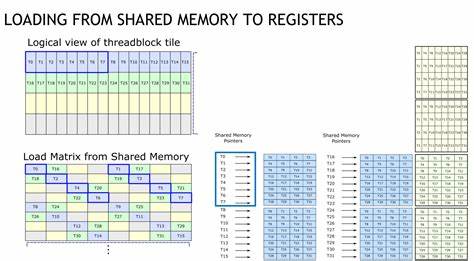
Преодолеть эти проблемы удалось путем внедрения нескольких критически важных оптимизаций. Во-первых, были применены векторизованные загрузки данных размером 128 бит (uint4), которые обеспечивают коалесцированные обращения к глобальной памяти по осям K в матрицах A и B. Такой подход значительно повышает пропускную способность загрузок, так как позволяет грузить сразу восемь элементов fp16 за один доступ. Во-вторых, в структуру размещения данных в разделяемой памяти была введена пермутация колонок с помощью XOR-операции. Такая перестановка устраняет конфликты банков при загрузке данных в регистры с помощью инструкции ldmatrix, так как она обеспечивает распределение обращений потоков в разные банковые группы, минимизируя замедления.
Благодаря этому доступы из shared memory стали почти полностью без конфликтов, что позволило снизить время простоя потоков в ожидании завершения передач данных. Дальнейшее улучшение производительности связано с организацией n-стадийного асинхронного конвейера передачи данных из глобальной в разделяемую память. PTX инструкция cp.async обеспечивает параллельное копирование данных без блокировки вычислительных потоков, давая возможность перекрывать загрузку данных с вычислениями. Использование cp.
async вместе с commit и wait_group позволяет строить конвейер, в котором следующая порция данных загружается, пока предыдущая обрабатывается, что ведет к более равномерному и эффективному использованию вычислительных ресурсов GPU. Важной стратегией также стало увеличение размеров выходных тайлов, которые вычисляет один warp за итерацию основного цикла. Расширение вычислительной нагрузки до 4x4 с учетом умножения и накопления за один проход позволило уменьшить количество синхронизаций и барьеров между потоками, что еще больше повысило производительность. В итоге достигнутая производительность стала практически равной показателям высокооптимизированной библиотеки cuBLAS: время выполнения задачи умножения матриц размером 4096x4096 снизилось до 895 микросекунд, а пропускная способность достигла 153.6 TFLOP/s, что составляет 93% от пиковой производительности GPU RTX 4090.
Однако при всей эффективности предложенного решения есть вопросы, которые требуют дальнейшего изучения. Например, несмотря на высокие показатели пропускной способности, метрики использования Tensor Core в инструментах профилирования иногда показывают меньшую, чем ожидалось, загрузку вычислителей. Это связано с оценочными допущениями в расчётах латентности, а также с возможными ошибками в инструментарии профилировщиков. Кроме того, наблюдаются конфликты при доступе к памяти, которые могут быть артефактами анализа, а не реальными узкими местами. В числовом плане использование fp16 для входных данных и fp32 для акмуляций дает хороший компромисс между скоростью и точностью.
Тем не менее, арифметика внутри mma инструкции обладает некоторой спецификой, которая может приводить к ошибкам округления. Для уменьшения этих погрешностей аккумулирование производится вне самой mma операции, что снижает суммарную ошибку до приемлемого уровня. Практическим результатом всех описанных подходов стала открытая реализация ядра матричного умножения, доступная на GitHub. Код максимально упрощен и ориентирован на понимание, что делает его хорошей отправной точкой для изучения оптимизаций Tensor Core и PTX программирования на архитектуре Ada. Опыт разработки и анализа данных ядер предоставляет важные инсайты для разработчиков CUDA и специалистов по оптимизации вычислительных задач.