Площадь единичного диска под однолистной функцией: глубокий анализ и практическое применение

Технология блокчейн

В математике комплексного анализа изучение отображений одиночных функций с области комплексной плоскости, таких как единичный диск, является фундаментальной задачей с широкими приложениями. Одним из ключевых вопросов является вычисление площади образа такого диска при преобразовании этим отображением. В частности, если функция является однолистной, то есть аналитической и взаимно однозначной на единичном диске, вопрос о площади образа приобретает точный аналитический смысл и может быть решен с помощью ряда Мёрса-Романса, или разложения по степеням переменной. Этот подход позволяет получить мощный инструмент для анализа сложных геометрических объектов, в том числе фрактальных множеств и объектов, возникающих в динамике комплексных функций, таких как множества Мандельброта и их подмножества. Однолистные функции на единичном диске играют центральную роль во всех ветвях комплексного анализа.

Они сохраняют структуру гладких отображений и обладают рядом свойств, которые упрощают изучение их геометрических характеристик. Основное свойство - аналитичность и инъективность - позволяет использовать метод изменения переменных для точного вычисления площади образа под действием функции. Рассмотрим такую функцию f, аналитическую и однолистную на единичном диске D:={ z ∈ К : |z|<1 }. Ее разложение в степенной ряд имеет вид f(z) = с_1 z + с_2 z² + с_3 z³ + ..

. При этом коэффициенты с_k играют ключевую роль в описании дифференциальных свойств образа и позволяют определить площадь множества f(D). Согласно классической теореме, площадь образа единичного диска при действии функции f выражается через сумму квадратов абсолютных значений коэффициентов ее степенного разложения, умноженных на силу соответствующей степени. В частности, площадь равна π × ∑_{k=1}^∞ k |c_k|^2. Такой результат становится следствием применения формулы Якобиана для комплексных функций и использования уравнений Коши-Римана, которые обеспечивают соответствующее упрощение вычислений.

 

Для наглядности легко представить интеграл площади в полярных координатах, что еще больше подтверждает данный вывод и делает расчет более прозрачным. Кроме теоретического значения эта формула имеет важное практическое применение. Например, рассмотрим задачу оценки площади облаков точек, получаемых в результате отображения геометрических фигур, которые порождаются динамическими системами или моделируются сложными аналитическими функциями. В частности, в теории фракталов и динамике комплексных систем широко изучается множество Мандельброта, которое содержит как подсеты с более простой структурой, так и весьма сложные формы. Один из таких подсетов - так называемое минималистское множество Мандельброта - получил широкое внимание благодаря своему относительному упрощению при сохранении основной геометрической организации.

 

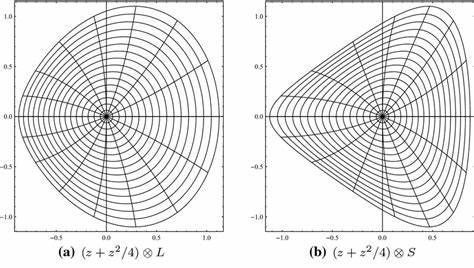
Рассмотрим окружность радиуса 1/4. Ее площадь равна π/16, что является простым аналитическим выражением. В то же время зеленая фигура - кардиоида - получается как образ множества { α : |α| < 1/2 } под отображением f(z) = z - z². Преобразование кардиоиды требует приведения области определения к стандартному единичному диску, что достигается масштабированием переменной. В результате разложение функции f(z) по степеням дает коэффициенты c_1 = 1/2, c_2 = -1/4.

 

Подстановка в основную формулу дает итоговую площадь, равную 3π/8. Суммарная площадь минималистского множества, включающего и окружность, и кардиоид, получается равна 7π/16, или приблизительно 1.3744. Эту величину удобно сравнивать с площадью всего классического множества Мандельброта, которая измерена экспериментально как примерно 1.5065.

Такое сравнение показывает, что минималистское множество составляет более 91% площади множества Мандельброта, что имеет как теоретическое, так и практическое значение в исследованиях в области комплексных динамических систем. При анализе функций, не обязательно удовлетворяющих условию инъективности, можно рассмотреть отображения вида f(z) = z^k. Тогда площадь образа единичного диска будет равна k π, что демонстрирует кратность покрытия исходной области. Таким образом, понятие кратности отображения связывается с геометрической характеристикой площади, что расширяет понимание взаимосвязей между алгебраическими свойствами функции и геометрией ее действия. Универсальность формулы площади через коэффициенты разложения позволяет применять этот подход во множестве смежных областей.

Например, при рассмотрении отображений, задающих воздушные профили (аэродинамические конструкции), можно прогнозировать свойства и характеристики объектов посредством оценки площади их образов. Это напрямую связано с задачами прикладной математики, инженерии и компьютерного моделирования, где аналитические методы помогают точнее понимать физические процессы. Также не стоит забывать об учебной мотивации: изучение комплексных функций с точки зрения площади и образов формирует глубокое осознание геометрии комплексного анализа. Концепция изменения переменных в интегралах, использование уравнений Коши-Римана, значение степенных рядов - все это становится более понятным и интуитивным благодаря таким наглядным примерам. Итогом является вывод, что вычисление площади образа единичного диска под действием однолистной функции - важная и интересная задача комплексного анализа, позволяющая объединить алгебраические, аналитические и геометрические методы.

Применение формулы, основанной на коэффициентах разложения функции, дает мощный инструмент исследования сложных фигур и динамических процессов. Благодаря этому подходу можно не только решать теоретические задачи, но и заложить основу для приложений в физике, инженерии и компьютерных науках. Таким образом, понимание площади единичного диска под однолистной функцией расширяет горизонты комплексного анализа и помогает глубже узнать природу отображений в комплексной плоскости, связывая при этом классические инструменты с современными приложениями. .