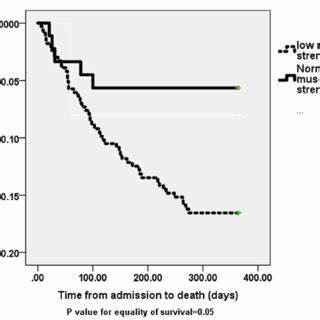
Понимание того, как изменяется уровень смертности с возрастом или продолжительностью какого-либо события, является одной из фундаментальных задач в статистике и демографии. Один из классических и весьма эффективных методов изучения этой динамики — построение логарифмической кривой выживаемости, где по оси абсцисс отражается возраст или длительность события, а по оси ординат — логарифм числа переживших этот временной отрезок. Такой подход был подробно описан Рональдом Фишером ещё в 1925 году и с тех пор стал неотъемлемой частью анализа жизни и смерти в различных областях – от биологии до социологии и даже анализа процессов в IT-сфере. Главная идея построения логарифмической выживаемости заключается в том, что скорость убыли количества живущих (или не завершивших событие объектов) пропорциональна текущему числу выживших. В результате на графике получается кривая, у которой касательная в любой точке отражает локальный уровень смертности или вероятность «смерти» события в этот момент.
При этом равномерное убывание с постоянной скоростью отображается графиком в виде прямой линии на логарифмическом масштабе. Это означало бы, что вероятность того, что объект «умрет» или событие завершится в любой момент времени, не зависит от возраста или продолжительности – то есть уровень смертности постоянен. Подобный подход позволяет сравнивать различные популяции, не поддаваясь искажениям из-за случайных колебаний и вариаций в выборках. В традиционных частотных гистограммах распределения количества умерших на каждый возраст подобные колебания могут легко скрыть общие тенденции, особенно если выборка относительно невелика. Логарифмическое отображение сглаживает эти влияния и позволяет сосредоточиться на более устойчивых паттернах.
Интересно, что в современной практике этот классический метод получил неожиданное применение, например, для анализа процессов в области разработки программного обеспечения. Рассмотрим пример с анализом времени открытия pull-запросов на GitHub — событием, которое в данном случае аналогично «смерти» объекта в классическом понимании. Время жизни pull-запроса — это срок от его создания до момента слияния (мерджа). Анализ двух популярных проектов показал, что большая часть запросов сливается довольно быстро – в течение нескольких часов, однако встречаются и «трудные» случаи, которые остаются открытыми продолжительное время. Таким образом, распределение времени ожидания напоминает тяжелый хвост – ситуация, когда редкие, но длительные процессы оказывают существенное влияние на средние показатели.
Подход Фишера предлагает уделить внимание именно «общему случаю» — исключить экстремальные, редко встречающиеся длинные задержки и сосредоточиться на временном отрезке, где сосредоточено большинство событий. Это дает возможность выявить скрытые закономерности, которые будут менее заметны при полном рассмотрении всех данных. В рассматриваемом примере фокус делается на интервале между 20 и 100 минутами ожидания — здесь сосредоточено больше всего данных и происходит интенсивное завершение pull-запросов. Построение графика зависимости логарифма числа выживших pull-запросов от времени показало, что линии для двух проектов практически прямые, что указывает на постоянный уровень событий в каждый момент времени — то есть вероятность слияния запросов стабильна в этом интервале. По углу наклона прямой можно оценить среднюю вероятность слияния за единицу времени.
В одном проекте эта цифра составляет около одного процента в минуту, в другом — примерно четыре процента. Это значение интерпретируется как средняя вероятность «смерти» в любой конкретный момент времени, что значительно облегчает понимание динамики процессов. Такая простая, но информативная статистика расширяет возможности управления временем рассмотрения и слияния pull-запросов, помогает выявить процессы, где происходит задержка, и в перспективе прогнозировать вероятность скорого закрытия либо затяжки работы с запросом в зависимости от его текущей «возрастной» стадии – продолжительности, в течение которой он открыт. Еще одна удивительная особенность анализа кривых выживаемости по Фишеру — это возможность интуитивно оценивать тип зависимостей, лежащих в основе рассматриваемых процессов. Если кривая логарифмической выживаемости является прямой линией, это указывает на постоянный уровень смертности, то есть вероятность события не зависит от времени.
Если линия кривой выгибается вниз, то это свидетельствует об увеличении вероятности события с возрастом — другими словами, возраст или время прямо влияют на повышение рискованности наступления «смерти». Напротив, если кривая изгибается вверх, это подразумевает спад смертности с ростом времени — становится менее вероятно, что событие завершится в поздние моменты. Возвращаясь к примеру с pull-запросами, анализ полных данных произвел интересные наблюдения. Первый проект демонстрировал закономерности, когда на ранних этапах вероятность слияния была высокой, но затем происходило выравнивание кривой, что показывало снижение скорости «смерти» — для долго открытых запросов вероятность мерджа уменьшалась. Второй проект в целом показывал почти постоянную вероятность слияния вне зависимости от возраста запроса, что позволяло утверждать, что время ожидания в нем является более надежным предиктором успеха запроса.
Понимание и применение этих методов имеет значение далеко за пределами демографии или IT. Анализ выживаемости с помощью логарифмических кривых может быть критичен для медицины, где отслеживают риск наступления определённых событий, например, смерти или рецидива болезни. Также это находит применение в страховании жизни, экономике, инженерии надежности и многих других областях, где важно предсказать вероятность возникновения события во времени. Важным аспектом статистики Фишера является также метод упрощения сложных вычислений, которые в его время невозможно было выполнить быстро, например, попытка узнать вероятность события в каждый единичный момент времени основывалась на логарифмировании сложных уравнений, что существенно сокращало вычислительную нагрузку и делало оценку доступной. Сегодня, с появлением мощных компьютеров и математического ПО, такие вычисления не представляют трудностей, но принципу разбивки проблемы на более простые части и использование логарифмических преобразований сохраняет свою актуальность.
Использование логарифмической выживаемости часто сопровождается рядом рекомендаций и предостережений, особенно при работе с реальными данными. Например, важно не бросать далеко в сторону редкие, но критические выбросы, не понимать их как незначительные, если они содержат важную информацию. Однако в некоторых ситуациях для фокусирования на доминирующих закономерностях и проверке гипотез такой подход имеет массу преимуществ. В итоге можно сказать, что концепции и методы, заложенные Рональдом Фишером почти сто лет назад, не потеряли своей универсальности и значимости. Логарифмическая выживаемость и анализ уровня смертности остаются критически важными для глубокого понимания процессов, лежащих в основе изменения численности популяций или событий с течением времени.
Они позволяют создавать модели, оценивать риски и принимать обоснованные решения как в научных исследованиях, так и в практических задачах разнообразных индустрий. Продвинутые методы статистики и математики, основанные на работах таких классиков, как Фишер, помогают нам не только проанализировать прошлое, но и лучше предсказывать будущее, оптимизировать процессы и уменьшать неопределенность, которая всегда сопутствует жизни и событиям в любой сфере. Поэтому понимание и применение логарифмических кривых выживаемости — это мощный инструмент в арсенале исследователя и специалиста, позволяющий раскрывать скрытые паттерны даже в самых сложных и объемных данных.