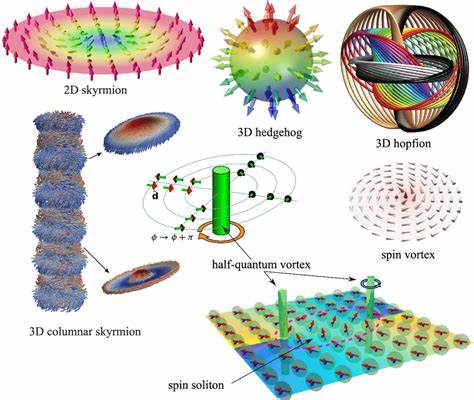
В современной науке о материалах топологические дефекты занимают центральное место в понимании механических и пластических свойств кристаллов. Очевидно, что в упорядоченных кристаллических решётках такие дефекты, как дислокации и дисклокации, служат микроскопическими носителями пластичности, отвечая за процессы деформации и разрушения. Однако многие реальные материалы, включая стекла и аморфные сплавы, лишены строгого периодического порядка, что поставило под вопрос возможность применения классических понятий топологии в их описании. Были ли топологические дефекты, аналогичные тем, что существуют в кристаллах, возможны в аморфных телах? Недавние исследования продемонстрировали, что ответ — да, и при этом новый тип топологических структур, получивший название «ёжиковые» топологические дефекты (hedgehog topological defects, HTD), становится ключевым элементом в описании пластичности трёхмерных аморфных систем. Аморфные твердые тела, к которым относятся стекла, полимеры и некоторые металлы, обладают сложной внутренней структурой, лишённой повторяющейся симметрии.
Именно отсутствие трансляционного периода затрудняет выявление классических топологических дефектов и связанной с ними микроскопической теории пластичности. Несмотря на это, в исследовании трёхмерных стекол были выявлены особые структуры в векторных полях, связанных с колебательными модами или динамическими отклонениями частиц, которые можно классифицировать как точечные топологические дефекты или «ёжики» — аналог ёжика с иглами, исходящими из точки. Такие дефекты характеризуются топологическим зарядом, инвариантным при гладких деформациях поля. Концепция ёжиковых топологических дефектов была заимствована из физики нематических жидких кристаллов и магнитных систем. Для трёхмерного нормированного векторного поля определён топологический заряд, вычисляемый интегралом по замкнутой поверхности, окружной такого дефекта.
Интересным отличием по сравнению с двумерными топологическими дефектами является то, что в трёхмерном случае знак топологического заряда не однозначен и не всегда информативен, поскольку векторное поле может быть инвариантным при изменении направления вектора на противоположное. Именно геометрия дефекта, а не лишь его топологический заряд, играет решающую роль в выявлении зон, склонных к пластическим перестройкам. В аморфных твердых телах с помощью компьютерного моделирования систем полимерного стекла было обнаружено, что такие ёжиковые дефекты могут носить либо радиальную, либо гиперболическую геометрию. Радиальные дефекты напоминают симметрично исходящие из точки векторы, в то время как гиперболические характеризуются наличием седлового распределения векторов. Важно отметить, что именно гиперболические ёжиковые дефекты демонстрируют сильную корреляцию с так называемыми «мягкими зонами» — локальными областями, где могут возникать структурные перестройки и пластические события.
Это открытие делает гиперболическую геометрию своеобразным маркером пластичности в трёхмерных аморфных средах. Для идентификации и классификации таких дефектов исследователи использовали дискретную схему на базе регулярной кубической сетки, на вершинах которой оценивалось направление векторного поля. С помощью численных методов вычислялся сумма внешних произведений и областей сферических треугольников, связанных с группами векторов на поверхности куба. Этот подход позволяет назначить каждой ячейке сетки количественную характеристику топологического заряда, а также определить геометрическую природу дефекта по количеству граней с отрицательным 2D-завихрением. Таким образом, отличить радиальные дефекты (без седловых граней) от гиперболических (наличие седловых граней) стало возможным.
Одним из основных полей для анализа являются собственные векторные поля гармонических колебаний системы, получаемые диагонализацией динамической матрицы. При низких частотах наблюдается квадратичное увеличение числа ёжиковых дефектов вместе с плотностью состояний, демонстрируя тесную связь между структурной топологией и динамикой. При этом обнаружено, что около значимых пластических событий ёжиковые дефекты с гиперболической геометрией концентрируются вблизи мягких зон, то есть пространственно локализованных областей с повышенной склонностью к структурным перестройкам. Не менее важным является исследование ёжиковых дефектов, выявляемых в полях ненормированного неаффинного смещения частиц при деформации аморфного тела, где прямо фиксируется динамическая активность, связанная с механическим ответом. Анализ таких полей позволяет не только локализовать зону предстоящих пластических событий, но и понять взаимосвязь между топологией и геометрией в реальном процессе деформации.
Отмечается, что, несмотря на отсутствие однозначного знака топологического заряда в этих полях, концентрация ёжиковых дефектов гиперболической геометрии чётко указывает на зоны пластической нестабильности. Эти результаты открывают интересные перспективы для экспериментальной диагностики и инженерного управления пластичностью аморфных материалов. Так как поле смещений можно измерять через современные методы компьютерной томографии, рентгеновской дифракции или микроскопии с высоким разрешением, возможность идентификации ёжиковых дефектов и связанных со структурными изменениями становится реальной. Кроме того, появление объяснимой и количественной связи между топологией векторных полей и макроскопическими механическими свойствами может способствовать разработке новых алгоритмов машинного обучения для прогнозирования долговечности и надёжности материалов. С точки зрения фундаментальной физики, выявление ёжиковых топологических дефектов в трёхмерных аморфных телах раскрывает сложный переплет топологических и геометрических свойств, отсутствующий в двумерных аналогах.
В частности, параллели между гиперболическими ёжиковыми дефектами в 3D и анти-вихрями с отрицательным числом завихрений в 2D показывают универсальность и богатство структурных феноменов в дисордерных системах. Более того, природа этих дефектов порождает вопросы о взаимодействии между ними, их динамике и влиянии на нелинейные механические отклики, а также связывает микроскопические характеристики с макроскопическим явлением текучести. На практическом уровне такой подход может изменить парадигму понимания пластичности в аморфных материалах, предлагая новые способы моделирования и предсказания поведения реальных инженерных систем. В отличие от традиционного измерения локальных структурных характеристик, основанных на статистике распределения частиц и их соседей, анализ более глубокой топологии и геометрии векторных полей предоставляет более надежные маркеры зон, склонных к разрушению и перестройкам. Исследования ёжиковых топологических дефектов в 3D аморфных материалах активно развиваются и уже влияют на разнообразные области, начиная от физики стекол и заканчивая разработкой новых полимерных и композитных материалов с заданными механическими свойствами.