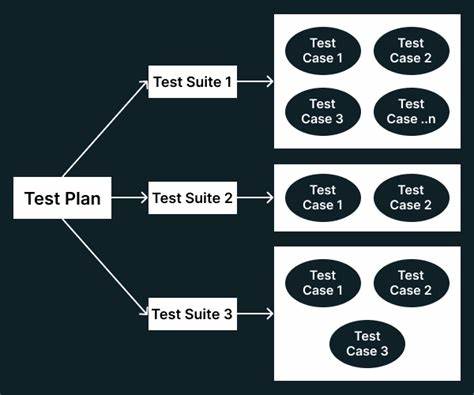
Тестирование программного обеспечения — неотъемлемая часть разработки, обеспечивающая качество и стабильность продукта. Однако иногда даже тщательно собранный набор тестов не гарантирует корректность реализованной функции. Случай, когда большие полиномиальные функции могут «обмануть» тестовый набор, показывает, что прохождение всех проверок — не всегда доказательство правильной работы алгоритма. Рассмотрим, как это возможно и к чему приводит такой нюанс в тестировании. Идея заключается в том, что если задать функцию, например, от трёх параметров, и известна её реализация на ограниченном наборе входных данных, то соответствующую полиномиальную функцию можно подобрать таким образом, чтобы она возвращала правильные значения для каждого теста.
При этом полином может быть невероятно сложным и в то же время не отражать реальной логики задачи. Примером служит подбор второго порядка полинома с коэффициентами, удовлетворяющего всем проверкам, построенного на базе SMT-солвера Z3. SMT (Satisfiability Modulo Theories) — это технология автоматического решения логических формул с учётом различных теорий, таких как арифметика, массивы, булевые значения. Солвер Z3 позволяет формулировать уравнения и условия, а затем искать значения переменных, которые удовлетворяют этим условиям. Используя этот инструмент, можно искать полиномы, удовлетворяющие набору входных значений и известных результатов функции.
Концептуально создаётся полином вида ax + by + cz + dxy + exz + fyz + a0, где x, y, z — входные параметры, а коэффициенты a, b, c, d, e, f и свободный член a0 — переменные, значения которых ищет солвер. Набор ограничений состоит в том, что для каждого конкретного входного триплета полином должен возвращать заранее известный результат, например максимум из трёх чисел. Когда таких ограничений достаточно много, можно последовательно отсеивать простые функции, такие как константы или выбор последнего элемента массива. Однако сложный полином, значительно больше и сложнее по структуре, способен пройти через все узкие ворота тестов, успешно их обманывая. Таким способом с помощью SMT можно даже автоматизировать подбор «правильного» полинома, который будет соответствовать любому написанному тестовому набору.
Это открывает интересную плоскость размышлений о самой природе тестирования и подходах к обеспечению качества кода. Тесты — это проверки совпадения поведения функции с ожиданиями на конкретных входах, но не обязательно полное описание логики. Чем более охватные и разнообразные тесты, тем труднее подобрать «обманный» полином, однако в теории любой конечный набор значений можно интерполировать с помощью полинома, как это известно из классической математики — например, по методу Лагранжа. Практическое применение такой техники остаётся скорее демонстрационным и педагогическим интересом. Тем не менее, она подчёркивает важность не слепо доверять прохождению тестов и рассматривать их как часть комплексного подхода к верификации.
Помимо юнит-тестов должны использоваться статический анализ кода, сложные системные тесты, а лучше — формальное доказательство корректности алгоритма. Также этот метод отражает ограничения тестирования методом «черного ящика», когда внутреннее устройство функции неизвестно, а проверка идёт только по входам и выходам. Маленький и простой набор тестов плохо защищает от переобучения или искусственно подобранных функций, которые не имеют практической ценности, но формально проходят. Поэтому разработчики должны тщательно продумывать не только входные данные, но и логику тестов, включая проверки граничных условий, отрицательных сценариев и свойств функций, таких как монотонность, симметрия и другие. Смогут ли инструменты на базе SMT и подобные техники автоматизировать этот процесс? Уже сегодня эти технологии помогают находить сложные решения в различных областях программирования и логики.
Автоматический подбор полиномов, функций и моделей, удовлетворяющих требованиям системы, — это ключевой тренд, который может изменить подход к разработке и тестированию. Запускать такой подбор можно как часть пайплайна автоматической сборки, где тестовый набор проходит через SMT-солвер, возвращающий модель функции, которая проходит все тесты. Но стоит помнить, что это как раз иллюстрация опасностей формального подхода без глубинного понимания задачи. В качестве образовательной задачи подбор полинома, обманывающего тесты, является отличным упражнением для освоения SMT-солверов, повышения грамотности в логике и методах поиска решений. Это помогает лучше понять, как работают современные инструменты формальной проверки и где их пределы.