Полярный момент инерции играет ключевую роль в механике и инженерии, особенно когда речь идет о сопротивлении материалов к кручению. Это фундаментальная величина, которая определяет способность тела противостоять воздействию крутящего момента, направленного вдоль оси объекта. Понимание и правильное применение полярного момента инерции крайне важно для проектирования вращающихся механизмов, валов, осей, а также других элементов, испытывающих торсионные нагрузки. Прежде всего, полярный момент инерции измеряет сопротивление объекта к torsion – процессу закручивания вокруг своей оси под действием приложенного крутящего момента. В отличие от простого трения или деформации сдвига, при кручении возникает сложная внутренняя перестройка распределения напряжений, которая зависит от формы и размеров поперечного сечения детали.
Физически полярный момент инерции отражает, насколько удалены от центра оси вращения отдельные элементы площади поперечного сечения. Чем дальше располагаются частицы материала, тем выше сопротивление крутящему воздействию, поскольку усилие распределяется по большему плечу. В отличие от момента инерции массы, который связывается с сопротивлением объекта к угловому ускорению и зависит от распределения массы, полярный момент инерции зависит от геометрии сечения, его формы и размеров, а не от материала, из которого сделан элемент. Полярный момент инерции обычно обозначается как J или I_z и измеряется в единицах длины в четвертой степени (например, м^4 в системе СИ). Если рассматривать отдельный элемент площади dA, удаленный на расстояние r от центра сечения, то его вклад в полярный момент инерции вычисляется как r^2 dA.
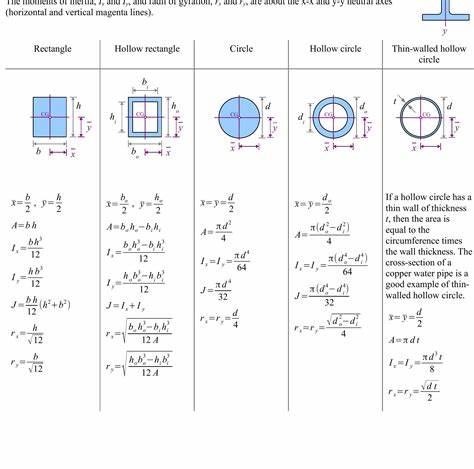
Чтобы получить общий полярный момент, необходимо интегрировать эту величину по всей площади поперечного сечения. Формулы для вычисления полярного момента инерции различаются в зависимости от формы сечения. Для круглого жёсткого вала это выражается формулой J = (π R^4) / 2, где R – радиус вала. Если вал полый, то формула принимает вид J = (π (R_1^4 – R_0^4)) / 2, где R_1 – внешний радиус, а R_0 – внутренний радиус полого вала. Для тонкостенных полых валов применяется приближенная формула, учитывающая толщину стенки t и средний радиус, что значительно упрощает расчеты, но при этом обеспечивает достаточную точность для многих инженерных задач.
Значение полярного момента инерции напрямую влияет на сопротивление крутящему моменту. Чем выше величина J, тем меньше угловое смещение и деформация при одинаковом крутящем моменте. Соответственно, чтобы повернуть вал с большим полярным моментом инерции, потребуется приложить более значительные усилия. В практике это помогает избегать чрезмерных деформаций и предотвращать повреждения оборудования, обеспечивая долговечность и надежность конструкций. Стоит отметить, что полярный момент инерции тесно связан с плоскими моментами инерции, относящимися к проекциям площади на ортогональных осях поперечного сечения.
Согласно теореме о перпендикулярных осях, полярный момент инерции равен сумме моментов инерции по двум взаимно перпендикулярным осям, лежащим в плоскости сечения. Эта взаимосвязь облегчает вычисления и дает глубокое понимание влияния геометрии сечения на механические свойства детали. Однако полярный момент инерции имеет свои ограничения. Его применение эффективно для расчета сопротивления кручению деталей с круглыми или близкими к круглым сечениями. В случаях, когда сечения имеют сложную или несимметричную форму, материалы могут испытывать так называемую деформацию вилкообразного типа, сопровождающуюся выпучиванием и выходом за пределы плоскости поперечного сечения.
Для таких случаев требуются более сложные методы анализа, учитывающие дополнительное искажение и распределение напряжений. В инженерной практике полярный момент инерции часто используется при проектировании валов электродвигателей, приводов, мостовых конструкций и других элементов, подвергающихся крутящим нагрузкам. Правильно рассчитанная величина позволяет обеспечить оптимальный баланс между прочностью, весом и экономичностью конструкции. Например, в машиностроении это помогает избежать усталостных разрушений, вызванных многократными циклическими нагрузками, и минимизировать вибрации и шумы при работе техники. Отдельно стоит упомянуть разницу между моментом инерции и полярным моментом инерции, что часто вызывает путаницу у новичков.
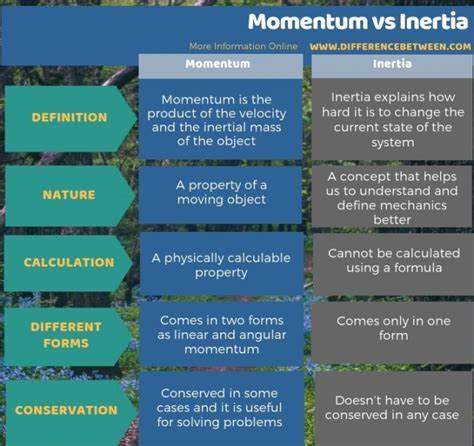
Момент инерции связан с сопротивлением объекта изменению угловой скорости и зависит от распределения массы по расстоянию от оси вращения. Этот параметр выражается в кг·м² и используется в динамике вращающихся тел. Полярный же момент инерции относится к сопротивлению кручению и зависит не от массы, а от геометрических параметров сечения, измеряется в м^4 и применяется в статике и прочности материалов. Для вычисления полярного момента инерции посредством интегрирования по площади используется формула, где учитывается расстояние каждого элементарного участка площади поперечного сечения до оси вращения. Те, кто желают быстро провести расчеты без сложных интегралов, могут применять табличные и эмпирические данные для стандартных сечений.
Полярный момент инерции также играет важную роль в анализе напряжённого состояния элементов конструкции. В сочетании с модулями сдвига материала он позволяет вычислять угловое смещение, определить максимальные касательные напряжения и оценить безопасность конструкции на этапе проектирования. Таким образом, знание величины J непосредственно сказывается на долговечности и надежности инженерных систем. В целом, полярный момент инерции является фундаментальным понятием при изучении сопротивления материалов и проектировании технических систем, подверженных крутящим нагрузкам. Он обеспечивает понимание того, как геометрия детали влияет на её прочность и деформативные свойства, и помогает инженерам принимать обоснованные решения при выборе материалов и форм сечений.
Чем больше и точнее значение этого параметра, тем надежнее будет конструкция при эксплуатации. Следует помнить, что несмотря на кажущуюся сложность определения полярного момента инерции, современные компьютерные программы и САПР значительно упрощают процесс анализа, позволяя быстро и точно рассчитывать необходимые характеристики изделий любого уровня сложности. В итоге, знание и правильное применение полярного момента инерции обеспечивает эффективное использование материалов, оптимизацию конструкции и повышение общей безопасности инженерных решений.