Фазовые переходы давно являются центральной темой в физике конденсированного состояния, и их объяснение традиционно опирается на теорию Гинзбурга-Ландау. Эта теория базируется на понятии параметра упорядоченности — величины, которая меняется с переходом системы между различными фазами, обычно связана с нарушением определенной симметрии. Однако современное исследование, проведённое профессорами Каноном Суном и Джозефом Мачейко, существенно расширяет понятие параметра упорядоченности, показывая, что он может иметь скрытую топологическую структуру. Это открытие создаёт новую парадигму для понимания фазовых переходов, связанных с топологией и симметрией одновременно. Классическая теория Гинзбурга-Ландау рассматривает так называемый свободный энерговой функционал как гладкую функцию от параметра упорядоченности.
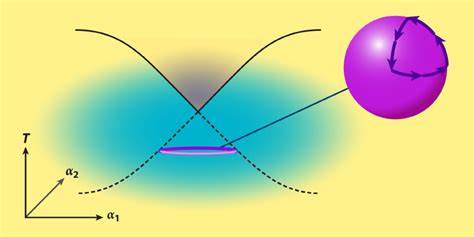
При изменении внешних условий, например температуры, минимумы этого функционала смещаются, что отображается в изменении величины параметра. Например, в случае обычного магнита, при понижении температуры ниже критической точки появляется ненулевая намагниченность, отражающая нарушение пространственной симметрии вращения. Выше критической температуры симметрия восстанавливается, и намагниченность равна нулю. Новым ключевым элементом, представленным в исследованиях Суна и Мачейко, является возврат топологии в описание параметров упорядоченности. Они показали, что множество параметров может быть расширено и включать дополнительные внутренние степени свободы, формируя сложный композитный параметр упорядоченности, который, в свою очередь, может обладать нетривиальной топологической структурой.
Это означает, что, проводя цикл в соответствующем параметрическом пространстве, система может аккумулировать глобальную геометрическую фазу, аналогичную фазе Берри, впервые описанной в 1984 году. Для наглядности рассмотрим модель, где температура и два дополнительных параметра управляют фазовой диаграммой. Такая система может существовать в двух фазах: симметрия сохраняется при высоких температурах, но нарушается при низких, что отражается в параметре упорядоченности. Когда исследователи проследили параметр вдоль замкнутого пути по дополнительным параметрам, они обнаружили, что параметр приобретает топологическую фазу — глобальное изменение, невозможное в рамках традиционной теории Гинзбурга-Ландау. Это уникальное свойство приводит к появлению квантованных топологических величин, таких как число завитков, которые устойчивы к малым возмущениям.
Топология в физике стала основным направлением после открытия квантового эффекта Холла и возникновения понятия топологических изоляторов и топологических металлов. Главное в таких системах — наличие топологических инвариантов, которые не зависят от локальных характеристик и обеспечивают устойчивость определенных свойств материала. Традиционно топология связывалась с электронными состояниями, однако работа Суна и Мачейко впервые доказывает, что и параметр упорядоченности самим по себе также может иметь топологический характер. Связь симметрии и топологии играет особую роль. Симметрии задают ограничения на поведение системы и её уравнений, а топология отвечает за глобальные свойства и новые стадии материи.
В своей работе учёные показали, что когда несколько разных упорядоченных фаз могут быть описаны одним и тем же неприводимым представлением симметрии, они могут взаимно обогащаться, образуя комплексный топологический параметр с богатой структурой. Особый интерес представляет применение этой теории к сверхпроводимости — явлению, при котором сопротивление материала падает до нуля ниже определённой критической температуры. В сверхпроводящих системах параметр упорядоченности отвечает за величину энергетического зазора, возникающего в спектре электронов. Исследователи доказали, что в таких системах могут сосуществовать несколько видов упорядочек с одинаковой симметрией, формируя композитный параметр, обладающий топологическими свойствами. Когда в сверхпроводнике сохраняется времяобратная симметрия, композиция параметров упорядоченности порождает так называемую фазу Берри равную π при прохождении по циклу в параметрическом пространстве.
Если же эта симметрия нарушается, система может демонстрировать аналоги топологических фаз, подобных Weyl-фермионам в топологических полупроводниках, с характерными точками касания энергетических зон и сопровождающими их числом завитков. Эти топологические особенности оказывают воздействие на макроскопические явления, такие как эффект Джозефсона — ток, протекающий между двумя сверхпроводниками через тонкий слой. Предсказанный эффект заключается в том, что текущий через джозефсоновский переход ток сохраняет свою величину после полного обхода контура в параметрическом пространстве, в отличие от традиционного сценария, когда ток меняет знак. Этот нетривиальный экспериментальный сигнал может стать ключевым подтверждением топологической природы композитного параметра упорядоченности и открыть новые направления для исследований в сверхпроводящих системах и квантовых технологиях. Новая топологическая вариация теории Гинзбурга-Ландау не только обогащает теоретические основы понимания фазовых переходов, но и расширяет возможности поиска материалов с уникальными свойствами, управляемыми топологией.