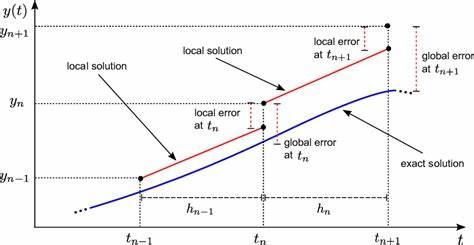
В математике доказательство является основой для утверждения истинности того или иного результата. Однако даже в самых продвинутых и кажущихся безупречными доказательствах порой скрываются ошибки, которые могут полностью подорвать их валидность. Разбираться в природе этих ошибок и уметь выявлять их крайне важно как для авторов научных статей, так и для рецензентов и всех, кто стремится к достоверности и точности в математике. Одним из распространённых взглядов на ошибки в математических доказательствах является их деление на «локальные» и «глобальные» ошибки, каждая из которых имеет свои особенности и методы определения. Локальные ошибки в математических статьях — это ошибки, связанные с конкретными отдельными шагами доказательства.
Доказательство, по сути, это цепочка логических выводов, где каждая связь должна быть безупречно обоснована. Возьмём упрощённый пример: предположим, что у нас есть утверждение «Если A, то B», а затем «Если B, то C», и мы делаем логический вывод, что «Если A, то C». Если хотя бы один из этих шагов содержит ошибку, то доказательство оказывается неверным. Локальные ошибки проявляются в том, что каким-то образом неверно заявлен или доказан отдельный переход, не выдержано условие, либо использована недостоверная гипотеза. Иногда локальную ошибку легко обнаружить, когда отдельный логический переход явно нарушен — например, утверждение, которое нельзя получить из предыдущих посылок.
Однако далеко не все локальные ошибки просты для восприятия или выявления. Некоторые локальные ошибки распространяются не на один шаг, а на небольшой кластер шагов, что усложняет их локализацию. Примером может служить циклический аргумент, когда доказательство замыкается на самом себе: утверждение A доказывается через B, а B — через A. Такой круг может выглядеть убедительно, но представляет собой фундаментальную ошибку логики. Стоит заметить, что циклы в доказательствах не всегда являются ошибками — их примером служат математические индукции, где проверяется базовый случай и затем доказывается переход.
Но ошибка возникает, когда подобный цикл не основан на аксиомах или базовых фактах, а просто использует утверждение для доказательства само себя. Ещё одна сложность локальных ошибок связана с неоднозначностью терминов и определений в доказательстве. Если математическое выражение или объект может интерпретироваться по-разному в разных частях доказательства, это приводит к несогласованности и, в конечном счёте, к ошибкам. Допустим, в одной части работы утверждают, что объект X имеет определённое свойство, основываясь на одной интерпретации, а в другой части ссылаются на вычисления, предполагающие другую трактовку этого же объекта. В таких случаях ошибка не локализуется на одном конкретном утверждении, а проистекает из общей неопределённости в формулировках.
Именно поэтому в математике особое внимание уделяется точным определениям, чтобы избежать подобных недоразумений и локализовать область применимости тех или иных утверждений. В отличие от локальных ошибок, глобальные ошибки носят более обобщённый характер. Их можно охарактеризовать как ошибки, воспринимаемые на уровне всего доказательства или даже всей теории. Глобальная ошибка проявляется, когда доказательство приводит к следствию, которое противоречит известным фактам или интуитивно неверно. Хорошим примером глобальной ошибки является наличие контрпримера к доказанному утверждению.
Если обнаружен такой контрпример, то уже гарантированно существует ошибка в доказательстве, пусть даже её конкретное местоположение пока не выявлено. Другой вариант — когда в доказательстве игнорируется или не используется гипотеза, которая является критически важной для утверждения. Такое упущение считается серьёзной глобальной ошибкой, поскольку доказывается не то, что предполагалось изначально, а более слабое или не соответствующее условию утверждение. Поиск глобальных ошибок часто оказывается более эффективным, особенно при работе с объёмными статьями. Для выявления локальных ошибок зачастую приходится внимательно читать и проверять множество строчек, что требует большого времени и углублённой концентрации.
Глобальную ошибку можно заметить, лишь просмотрев структуру доказательства, поняв его ключевые предпосылки и ожидаемые результаты. Если общий вывод кажется необоснованным или противоречит предварительным знаниям, это уже повод тщательно пересмотреть доказательство на предмет ошибок. Различие между локальными и глобальными ошибками важно также для понимания того, как именно следует строить доказательство. В идеале доказательство должно быть устойчивым к локальным ошибкам, чтобы даже в случае незначительных огрехов его основная идея оставалась незатронутой и полезной. Подобный подход характерен для методов «разбиения на части» — когда большая задача разделяется на несколько меньших, и даже если один из подходов не сработает, остальные части доказательства сохраняют ценность.
В противоположность этому глобальные ошибки часто требуют фундаментального пересмотра стратегии доказательства — если вывод противоречит известным фактам, просто исправить отдельные шаги недостаточно, необходимо изменить общую логику или гипотезы. Нередко глобальные ошибки выявляются через «метод параллельного рассуждения». В этом подходе предполагается, что если доказательство утверждения A состоит из цепочки шагов, то аналогичные шаги должны работать для некоторого похожего утверждения B. Если же для B найден контрпример или доказательство невозможно, это ставит под вопрос корректность цепочки для A. Такой худо ли, тёмно ли подход помогает выявлять уязвимости в построениях без детального локального анализа.
Стоит особо подчеркнуть, что тестирование доказательств на ошибки и создание самих доказательств — разные задачи, требующие различных стандартов строгости. При написании доказательства математики стремятся к максимально строгой и прозрачной логике, где каждый шаг тщательно обоснован. В то время как при поиске ошибок допускается применение эвристик, перестановок и даже интуитивных рассуждений, чтобы быстро выделить проблемные места. Это объясняется тем, что опровержение — задача поиска хотя бы одного изъяна, а не построения полной цепочки. Иногда обнаруженная кажущаяся ошибка может указывать не на невыполнимость доказательства, а на необходимость пересмотра устоявшихся математических интуиций.
Интересно заметить, что глобальные ошибки часто оказываются более разрушительными и серьезными, чем локальные. Если локальную ошибку удаётся исправить или обойти, перестроив отдельные этапы доказательства, то глобальная ошибка угрожает самому смыслу и корректности результата. Именно потому дешёвый аргумент «у меня есть две версии доказательства» не останавливает тех, кто обнаружил контрпример, — наличие контрпримера мгновенно отвергает любые изложенные варианты, независимо от их количества или тонкости. Важно отметить и роль ясности и точности в математическом изложении как средства профилактики ошибок обоих типов. По мере того как доказательства становятся всё более сложными и громоздкими, особенно в области высоких уровней абстракции, трудно избежать логических пробелов и двусмысленности.
Поэтому аккуратное определение понятий, последовательное изложение шагов, а также чёткая структура доказательства способствуют как выявлению ошибок, так и повышению качества самой работы. Математическое сообщество ценит культуру критического анализа и коллективной проверки доказательств. Опубликованные работы проходят экспертизу и рецензирование, но в более сложных и значимых случаях, таких как знаменитые нерешённые задачи или крупные теоремы, доказательства проверяются и обсуждаются многими специалистами. Именно они помогают выявить локальные и глобальные ошибки, способствуют уточнению и совершенствованию представленных результатов. В итоге, понимание различий между локальными и глобальными ошибками и методов их выявления играет ключевую роль в математическом творчестве.
Это не только повышает качество научных публикаций, но и способствует научному прогрессу, позволяя отделять прочные теоретические основы от ошибочных построений. Авторы, рецензенты и читатели, вооружённые таким знанием, работают над тем, чтобы математика оставалась точной, логически стройной и надёжной наукой, свободной от неточностей и заблуждений.