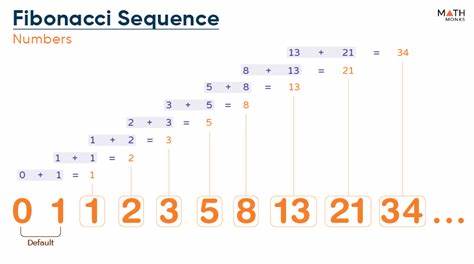
Последовательность Фибоначчи является одним из наиболее известных и удивительных явлений в области математики и природных наук. Она начинается с двух чисел 0 и 1, после чего каждое последующее число формируется как сумма двух предыдущих: 0, 1, 1, 2, 3, 5, 8, 13 и так далее. На первый взгляд, эта последовательность кажется простой и изученной, однако при глубоком анализе открываются ее загадочные взаимосвязи с фрактальной структурой и природными процессами. Число Fib(50), которое равно 12 586 269 025, занимает важное место в изучении последовательности Фибоначчи, поскольку оно демонстрирует экспоненциальный рост и сложность, присущую этой числовой серии. Раскрыть внутренние отношения Fib(50) помогает применение диаграмм, которые визуализируют данное число как часть большой фрактальной системы, подчеркивая регулярность и повторяемость, характерные для фракталов.
Фракталы — это объекты, обладающие свойством самоподобия, где структура повторяется на разных масштабах. В последовательности Фибоначчи можно наблюдать именно такую самоподобную природу: каждое число строится из двух предыдущих, а сама последовательность отражает бесконечный процесс деления и масштабирования. Если представить число Fib(50) в виде диаграммы, то видна разветвленная структура, где каждая ветвь иллюстрирует предыдущие значения и их зависимость друг от друга. Данный подход к визуализации позволяет не только глубже понять арифметическую суть последовательности, но и увидеть ее связь с природными паттернами. Примером может служить раковина наутилуса, расцветка листьев, расположение ветвей у деревьев и архитектура сердечных сокращений — все эти процессы подчиняются принципам роста, похожим на последовательность Фибоначчи и ее фрактальную природу.
Диаграммы, отображающие Fib(50), демонстрируют, как растущая числовая последовательность становится основой для создания сложных структур. Эти визуальные образы не ограничиваются математикой или теорией чисел — они применяются в биологии, инженерии, искусстве и даже цифровых технологиях. К примеру, фрактальная визуализация помогает в моделировании природных объектов и способах оптимизации процессов в компьютерных алгоритмах. Число Fib(50), полученное как сумма Fib(49) и Fib(48), равно 7 778 742 049 плюс 4 807 526 976. Их соединение на диаграммах иллюстрирует базовую формулу последовательности Фибоначчи: F(n) = F(n-1) + F(n-2).
При этом диаграмма позволяет проследить каждый уровень суммирования от начальных значений до 50-го члена, раскрывая удивительный мир повторяющихся структур и завораживающих узоров. Особое внимание вызывает связь последовательности с золотым сечением — числом, к которому стремится отношение соседних чисел Фибоначчи при увеличении индекса. Эта связь способствует изучению пропорций в архитектуре, живописи и природе, а визуальные представления на диаграммах лишь подтверждают гармонию и эстетику, заложенные в математической последовательности. Изучение Fib(50) через диаграммы не просто расширяет понимание числовых закономерностей, но и играет важную роль в образовательных и исследовательских проектах. Использование специализированных инструментов и сервисов визуализации позволяет создавать интерактивные модели, которые делают сложные математические концепции доступными для широкой аудитории.