Обнаружение столкновений является одной из ключевых задач в разработке современных игр и систем симуляции физики. С момента появления алгоритма Гилберта-Джонсона-Кирти (GJK) в 1988 году он стал неотъемлемой частью большинства популярных игровых движков и используемой технологией для определения, пересекаются ли объекты в трехмерном пространстве. Несмотря на то что GJK традиционно рассматривается с геометрической точки зрения, в последние годы все больше внимания уделяется его формализации как задачи оптимизации, а именно – как частному случаю метода Франк-Вульфа (Frank-Wolfe, FW). Понимание этой связи открывает новые перспективы для повышения эффективности алгоритмов обнаружения столкновений и развития систем игрового и виртуального взаимодействия. Алгоритм GJK изначально был разработан как геометрический метод для нахождения минимального расстояния между выпуклыми множествами, сегментами или полигонами.
Его логика строится вокруг понятия разности Минковского, то есть рассмотривания множества точек, которые можно получить вычитанием одной фигуры из другой. В рамках этой геометрии алгоритм итеративно добавляет в активное множество новые точки-опоры для сужения приближения к минимальному расстоянию. Традиционные объяснения GJK базируются на деталях работы с этими геометрическими объектами и динамическом обновлении простого сопряженного множества. Однако в области математической оптимизации существует давно известный метод Франк-Вульфа, сформулированный еще в середине XX века, который решает задачи поиска экстремумов выпуклых функций с ограничениями в виде выпуклых множеств. Метод FW характеризуется итеративным поиском и улучшением приближения оптимального решения посредством выбора направлений, где функция уменьшается, с последующей аппроксимацией результата.
Удивительно, но именно эта алгоритмическая схема лежит в основе GJK, несмотря на то что об этом редко говорится в игровой индустрии и в технической документации движков. Современные исследования 2022 года явно связали алгоритм GJK с методом Франк-Вульфа, показывая, что GJK можно рассматривать как специализированную реализацию FW с расширенной активной точечной сеткой, представляющей текущее приближение. Это означает, что GJK не только эффективно комбинирует геометрические методы, но и использует мощь оптимизационных процедур для минимизации расстояния между фигурами. Такое понимание позволяет применять более обширные инструменты оптимизации для улучшения сходимости и уменьшения вычислительных затрат, что особенно важно в реал-тайм системах с высокой нагрузкой. Преимущество подхода, рассматривающего обнаружение столкновений как задачу выпуклой оптимизации, состоит в универсальности и математической строгости.
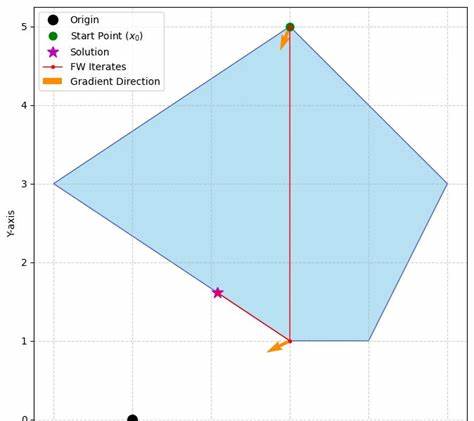
Вместо того, чтобы ограничиваться сугубо геометрическими построениями, разработчики могут использовать классические методы оптимизации с гарантией сходимости и известной оценкой точности. При этом проблемы, которые кажутся сложными с геометрической точки зрения, становятся естественными и понятными через призму алгебраических и аналитических инструментов. Связь GJK с FW становится особенно заметна при разборе конкретных шагов алгоритма. Метод FW в классическом варианте итеративно находит направление движения, максимизируя линейную аппроксимацию градиента функции на множестве допустимых значений, а затем выполняет проекцию или релаксацию, приближаясь к точке минимума. В GJK эти операции эквивалентны поиску опорной точки в направлении, определяемом текущей оценкой градиента расстояния, и проекции на выпуклую оболочку множества поддерживающих точек.
Такая интерпретация упрощает понимание работы алгоритма, одновременно позволяя улучшить его путем внедрения методов «активных подмножеств» или «полноэкспоненциальной коррекции», что снижает число итераций и ускоряет вычисления. Традиционно большинство материалов по GJK, будь то книги, видео или статьи, фокусировались на объяснении через визуализацию и геометрические рассуждения, что помогало понимать алгоритм новичкам и разработчикам. Однако это ограниченное восприятие мешало интеграции достижений из области оптимизации, которые давно наработаны математиками и применяются в других сферах, таких как машинное обучение, исследование операций и эконометрика. Публикация 2022 года впервые подробно изложила такие связи, отмечая, что возможности для дальнейшего улучшения GJK еще есть и что разнообразие оптимизационных техник может привнести прорывные изменения в вычисление столкновений. Подход через оптимизацию также знаменует собой переход от эвристик и специфики реализации к более формальным основам.
Благодаря этому можно проводить теоретический анализ скорости сходимости, устойчивости к погрешностям и масштабируемости. Кроме того, методы из области оптимизации предоставляют инструменты для параллелизации вычислений и адаптации к высокопродуктивным вычислительным системам, что важно для разработки игр с высоким уровнем детализации и реалистичной физикой. Стоит отметить, что классический метод Франк-Вульфа известен с середины 1950-х годов и применялся в самых разных областях. Его использование для задачи минимизации расстояния между выпуклыми множествами позволяет обобщить алгоритм GJK и рассматривать его как частный случай более универсального решения. По историческим данным, сходство между этими алгоритмами выявлялось еще в поздних 70-х и в начале 2000-х, но прежде информация оставалась в основном в сообществе исследователей оптимизации и геометрии, не выходя на уровень широкого применения в игровых технологиях.
Возможно, разделение между геометрами и оптимизаторами объясняет почему данный фундаментальный факт долгое время оставался вне поля внимания разработчиков. Еще одним важным аспектом является то, что алгоритм GJK с точки зрения метода Франк-Вульфа можно рассматривать как итеративное уточнение при помощи расширения множества точек в активном наборе. В классическом варианте FW используется лишь простая линия для обновления приближения, что при сложных конфигурациях приводит к замедленной сходимости или «змеевидным» движениям. В GJK же расширение актива до простого симплекса и последующая проекция на выпуклую оболочку дают значительно более быстрый и устойчивый результат, что критично при обработке столкновений в реальном времени. Для разработчиков и инженеров, работающих со сложными сценами и множеством объектов, понимание этих нюансов открывает дорогу к разработке более гибких и производительных систем обнаружения столкновений.
Кроме того, осознание GJK как реализации метода FW способствует более прозрачной интеграции с другими модулями оптимизации в игре, например, для задач навигации искусственного интеллекта, процедурной генерации или физического моделирования материалов. Перспективы использования оптимизационного взгляда на обнаружение столкновений расширяются выходом новых исследований и инструментов, направленных на улучшение алгоритмических схем. Дополнение GJK методами сглаживания, инерционными механизмами и адаптивным выбором активных подмножеств способно повысить надежность и быстрое реагирование системы при высоких нагрузках. Наряду с этим растет понимание важности использования специализированных численных методов решения подзадач проекций, что снижает вычислительную стоимость каждого шага и делает возможным масштабирование на многопроцессорных и графических вычислительных платформах. Необходимо подчеркнуть, что подобный переход от интуитивной геометрии к строгой математической оптимизации не противоречит классическим представлениям о GJK, а, напротив, обогащает их.