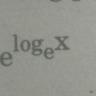Масштабирование классических алгоритмов и трюков для работы с гигантскими объемами данных становится ключевой задачей в современной науке и промышленности. Один из известнейших и часто используемых приемов — трюк XOR, позволяющий быстро выявить пропущенные или отличающиеся элементы между списками или множествами. Однако данный метод хорошо работает лишь с небольшими наборами или с ограниченным числом отличающихся элементов. Как же его расширить для обработки миллиардов строк, выявляя тысячи или даже десятки тысяч различий? Ответ кроется в структуре данных, известной как инвертируемый фильтр Блума, которая обладает впечатляющими свойствами по сравнению и восстановлению разницы между большими наборами при минимальных затратах по памяти и времени. Классический трюк XOR основывается на том, что при последовательном применении операции исключающего ИЛИ (XOR) к всем элементам списка, из которого удалены одно или два значения, можно легко выявить пропущенные значения.
Однако когда количество пропущенных элементов растет, а их количество неизвестно заранее, данный подход начинает терять свою эффективность. На первом уровне расширения можно попытаться разбить множество на несколько частей с помощью функции хеширования и применить XOR к каждой части отдельно. Идея состоит в том, чтобы разбить исходные данные так, чтобы в каждой корзине было не больше одного отличающегося элемента, и тогда трюк XOR на каждой корзине снова будет работать. Однако на практике равномерное распределение элементов редко достижимо, и часто корзины могут содержать несколько отличий, что сделает восстановление невозможным. Чтобы справиться с этой проблемой, необходим более продвинутый способ, который позволил бы не только выявлять отличие, но и эффективно восстанавливать уникальные элементы при больших масштабах.
Здесь на сцену выходят инвертируемые фильтры Блума (IBF). Они вобрали в себя преимущества классических фильтров Блума, применяемых для быстрого и экономного хранения множества с вероятностной проверкой принадлежности элементов, и добавляют возможность декодирования для получения конкретных значений, которые различаются в сравниваемых множествах. Инвертируемый фильтр Блума представляет собой массив ячеек, каждая из которых хранит три основные поля: сумму XOR значений элементов (idSum), сумму XOR их хешей (hashSum) и счетчик количества элементов (count). Каждый элемент множества при добавлении в IBF помещается в несколько ячеек, определяемых с помощью нескольких хеш-функций. Когда необходимо сравнить два множества, два инвертируемых фильтра строятся соответственно, а затем значения одной структуры вычитаются из другой.
Элементы, присутствующие в обоих множествах, взаимно уничтожаются на уровне XOR и счетчиков. В итоге остается фильтр, который отражает именно симметрическую разницу множеств. Ключевой особенностью IBF является процедура декодирования, которая идет по сложному графовому алгоритму, называемому "очисткой" или "отшелушиванием". Принцип состоит в нахождении ячеек с чистым содержимым, то есть тех, где счетчик равен плюс или минус один, а сумма XOR и хеш суммы совпадают корретно. Такие ячейки указывают на уникальный элемент в одну из множеств, который после его извлечения и вычитания из других ячеек открывает новые "чистые" ячейки.
Итеративно повторяя этот процесс, можно восстановить полный набор уникальных элементов, входящих в разницу. Для успешной работы IBF важно правильно подобрать количество ячеек и количество хешей, чтобы вероятность коллизий и ошибок была минимальной. Обычно, чтобы справиться с симметрической разницей размера d, требуется фильтр в размере примерно 1.2–1.3 раза больше дельты.
В этом случае декодирование работает с весьма высокой вероятностью успешно. Преимущество инвертируемых фильтров Блума в том, что их размер и сложность зависят только от величины разницы между множествами, а не от их общего размера. Это дает возможность эффективно справляться с миллиардами строк, если их отличия не слишком велики. Такие возможности крайне полезны в базах данных, распределенных системах, системах хранения и облачных платформах, где сравнивать и синхронизировать огромные объемы данных ежедневно становится важной задачей. Задача быстрого и экономного выявления отличий между двумя наборами данных называется задачей согласования множеств (set reconciliation).
Ранее предлагались алгоритмы на полиномиальной основе и методы, опирающиеся на кодирование ошибок. Современный подход с использованием IBF устойчиво конкурирует с ними, предлагая уникальное сочетание эффективности, простоты реализации и удобства масштабирования. С практической точки зрения, реализация инвертируемых фильтров Блума требует аккуратного подбора хеш-функций и оптимизации операций XOR, чтобы минимизировать коллизии и ускорить процесс кодирования и декодирования. Несмотря на сложность концепции, базовую реализацию можно выполнить относительно просто и встроить в существующие системы. Некоторых компенсирует тот факт, что на данный момент нет большого количества хорошо зарекомендовавших себя, поддерживаемых библиотек IBF, но это направление активно развивается.