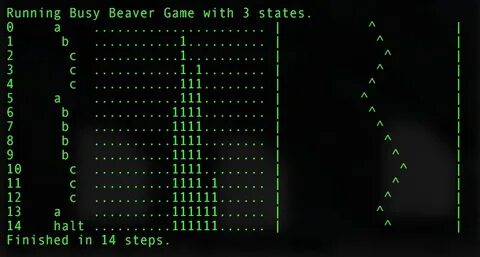
Функция Busy Beaver занимает особое место в теории вычислимости и автоматов, являясь одним из самых загадочных объектов, введённых классиком Тибором Радо в 1962 году. Она демонстрирует глубину и сложность фундаментальных вопросов вычислений, став символом пределов алгоритмических возможностей. Впервые в истории после более чем сорока лет застойных исследований было официально и формально доказано значение пятого Busy Beaver, что стало настоящим прорывом в области теоретической информатики и логики. Это достижение подтверждает не только сложность задач вычислимости, но и силу коллективных усилий, использующих современные формальные методы и компьютерные доказательства. Busy Beaver - это функция от числа состояний машины Тьюринга с двумя символами, которая описывает максимальное количество шагов, которые такая машина может выполнить, начиная с пустой ленты, прежде чем остановиться.
Несмотря на простоту определения, вычисление значений этой функции выходит за пределы традиционных вычислительных методов из-за своей невычислимой природы. Считается, что значения функции растут очень быстро, и даже для машин с малым числом состояний точное значение трудно определить. Последнее до недавнего времени подтверждённое значение - это четвёртое значение Busy Beaver, которое известно с 1980-х годов. Теперь в научном мире появился новый рубеж: пятого значения. Проект по определению пятого значения Busy Beaver представлял собой колоссальную трудоёмкую задачу.
Исследовательская группа под названием bbchallenge включала в себя специалистов из разных стран и дисциплин, объединившихся ради решения одной из самых сложных проблем современной теоретической информатики. Команда перебрала, проанализировала и формально доказала поведение более 181 миллиона машин Тьюринга с пятью состояниями. Это требовало невероятного вычислительного ресурса, а также разработки новых методов формального доказательства, которые позволяли безошибочно классифицировать машины по принципу "останавливаются" или "не останавливаются". Доказательство, выполненное с помощью системы Coq - интерактивного доказательного помощника, - стало весомым вкладом в проверяемую наукоёмкость, гарантируя корректность и полноту результата. Применение Coq позволило формально зафиксировать все этапы анализа, исключая человеческие ошибки и обеспечивая повторяемость эксперимента.
Формальное доказательство вывело верификацию вычислительных феноменов на новый уровень, показав, что даже крайне сложные задачи с элементами недоказуемости могут подвергаться строгому математическому анализу. Результаты, полученные группой bbchallenge, имеют широкий резонанс не только в области теоретической информатики, но и в смежных научных областях. Изучение поведения машин Тьюринга тесно связано с проблемами алгоритмической сложности, математической логики и модели вычислений. Новый результат стимулирует развитие новых техник анализа и алгоритмов, которые могут найти применение в робототехнике, криптографии и даже философских исследованиях природы сознания и мышления. Определение пятого значения Busy Beaver подтверждает уникальные свойства невычислимых функций и служит красноречивым примером пределов формальных систем.
Эта работа продемонстрировала, насколько масштабные коллективные проекты совместно с автоматическими доказательными системами способны разрешать задачи, которые ранее считались недостижимыми. Массовое онлайн-сотрудничество, что хорошо видно на примере bbchallenge, становится новым стандартом научного исследования в эпоху цифровой трансформации, позволяя объединять знания, опыт и ресурсы для прорывных открытий. За последние десятилетия представления о вычислимости и алгоритмах значительно расширились. Появление современных формальных систем доказательств, вычислительных кластеров и распределённых вычислений позволяет глубже исследовать классические проблемы и находить ответы на вопросы, поставленные ещё в золотую эру теории алгоритмов. Открытие значения пятого Busy Beaver - это не только важный этап в развитии математики и информатики, но и вдохновляющий пример того, как теория и практика могут работать рука об руку, преодолевая барьеры непознаваемости.
Подводя итог, определение пятого значения функции Busy Beaver - это уникальное событие, объединяющее теорию вычислений, современные технологические средства и глубокий интеллектуальный труд. Этот результат не только расширил наши знания о пределах алгоритмов, но и придал новое значение формальному подходу в науке, формируя будущее исследований в области вычислительной математики и логики. Благодаря таким открытиям становится ясно, что даже в век высоких технологий остаются фундаментальные научные задачи, которые требуют творческого, коллективного и технически точного подхода для их решения. Эти открытия продолжают задавать тон будущим поколениям учёных и инженеров в эпоху беспрецедентных технологических изменений. .