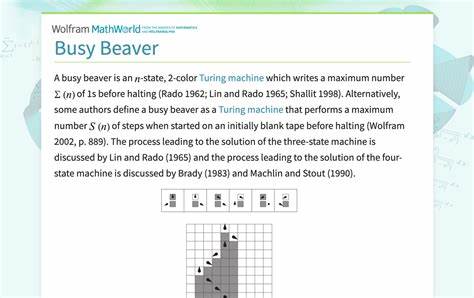
Функция Busy Beaver — одна из самых загадочных и захватывающих тем в теории вычислимости и математической логике. Она определяет максимальное количество шагов, которое машина Тьюринга с заданным числом состояний может выполнить, прежде чем остановиться, если запустить её на пустой входной ленте. Подобные значения растут невероятно быстро, они далеко выходят за рамки привычной математики и заставляют пересматривать наши взгляды на границы вычислимости и математики в целом. В последние годы внимание специалистов привлекает седьмая функция Busy Beaver, особенно ее шестое значение, известное как BB(6). Впервые было показано, что этот параметр не просто большой, а колоссально огромный — настолько, что представлял сложность для человеческого понимания и математического описания.
Если для машин с пятью состояниями максимальная длина вычисления до остановки измеряется в десятках миллионов шагов, то для машин с шестью состояниями эта величина взрывается до величин порядка \(10^{10^{10^{...}}}\) с десятками миллионов вложений экспоненциальной операции, что выходит далеко за пределы вычислимых чисел даже в их самых абстрактных интерпретациях. Прогресс в понимании BB(6) стал возможным благодаря командной работе и использованию продвинутых доказательных систем, таких как Coq, которые позволили уверенно подтвердить эти поразительные оценки.
Ранее оценка BB(6) ограничивалась сравнительно «маленьким» значением порядка 10^{36,534}, что, само по себе, уже казалось огромным. Однако были получены результаты, которые увеличили нижние оценки до степеней, сравнимых с десятками миллионов итераций сверхэкспоненциальных операций, а потом и до сложных иерархий функций, таких как тетрация и пентация. Это означает, что BB(6) больше 2^{2^{2^{...
}}} с девятью количественными вложениями экспонент — минимальный пример того, насколько быстро может расти такая функция. Нельзя недооценивать серьёзность этих открытий — именно они поднимают вопросы о том, где и как пределы математики и доказуемости встречаются с фундаментальными вопросами логики и науки о вычислениях. Известно, что значения BB для достаточно больших параметров становятся независимыми от классических аксиоматических систем, таких как ZFC (Zermelo-Fraenkel теория множеств с аксиомой выбора). И если BB(6) уже сейчас достигло настолько огромных значений, что оценка возможна лишь через сложные, неинтуитивные иерархии, то возникает обоснованное предположение, что независимость от аксиоматики ZFC может проявляться уже на гораздо меньших значениях, возможно даже для размеров машин с 7–9 состояниями. Данная ситуация подтверждает глубокое взаимодействие между теорией вычислимости, теорией сложности и математической логикой.
Значения функции Busy Beaver напрямую связаны с проблемами остановки и алгоритмической неразрешимости, а также с фундаментальными пределами формальных систем доказательств. Всё это является не просто технической метаматематикой, а даёт понимание того, что в математике есть нерешаемые вопросы, которые даже при самом мощном формальном аппарате не удастся разрешить. Большой интерес к BB(6) вызван не только вызовами, которые она создаёт для теории, но и новыми методами, которые используются для её анализа. Современные исследования применяют не только традиционные математические доказательства, но и компьютерные доказательные системы, где автоматизированные доказательства служат подтверждением невероятной длины вычислений, а тщательно сконструированные программы проверяют логику работы машин. Появляются программы, способные оперировать сложнейшими функциями роста, такими как тетрация — повторное возведение в степень — и даже пентация, превосходящая тетрацию по скорости роста.
Отмечается удивительная связь между машинами с шестью состояниями и вычислительными феноменами, напоминающими коллатциевские процессы — последовательности чисел с запутанным поведением, остающимся пока неразрешённым в математике. Многие из чемпионов BB(6) можно описать как машины, обрабатывающие входные переменные с помощью экспоненциальных или вышеуровневых вычислений, которые повторяются и сопровождаются сложными проверками. Такое поведение создает огромные числа шагов, прежде чем машина остановится, и пока мы можем строить нижние оценки этих чисел, верхние оценки остаются открытыми. В научном сообществе вызывает резонанс идея, что важные значения функции Busy Beaver, включая BB(6) и BB(7), могут быть настолько велики, что невозможно выразить их привычными математическими средствами. Появляется вероятность, что для этих величин будет нужно прибегать к гипероперациям или даже к вышестоящим уровням в арифметике больших чисел.
Зачем это важно? Потому что это подчеркивает фундаментальные ограничения не только вычислительной техники, но и самой формализации математики. С другой стороны, этот мощный рост функции показывает, что даже при добавлении одного состояния вычислительной машине открываются новые возможности для экспоненциального (и даже сверхэкспоненциального) расширения вычислений. Таким образом, шестое состояние — своеобразный «прыжок» в бесконечность, то место, где рост оценок становится поистине фантастическим. Стоит также упомянуть дискуссии в научном сообществе о том, что не все виды вычислений, которые приводят к огромным числам, имеют простой или ясный механизм. Например, экспертам известно, что в BB(6) полно так называемых «криптид» — машин, поведение которых кажется статистически замирающим, словно они должны остановиться, но доказать это очень трудно.
Такие машины обнаруживают тончайшие арифметические зависимости, зачастую связанные с трудноразрешимыми гипотезами вроде Коллатца. Их изучение помогает не только в понимании BB, но и стимулирует развитие новых областей теоретической математики. По мнению многих специалистов, дальнейшие улучшения нижних границ для BB(6) и BB(7) будут связаны с конструкцией все более сложных машин и выявлением соответствующих им функций с ростом, выходящим далеко за пределы человеческого понимания. Это открывает захватывающий фронтир — одновременное столкновение между вычислительной мощью минималистичных формальных систем и границами доказательности. Фундаментальный вопрос, который возникает после изучения BB(6), связан с тем, в какой степени значения функции Busy Beaver становятся независимыми от базовых формальных систем, таких как ZFC.
Известно, что при достаточно большом значении параметра n значения BB(n) невозможно доказать или опровергнуть в рамках этих систем. Постепенно появляется гипотеза, что порог такой независимости гораздо ниже, чем считалось ранее. Это предполагает, что загадочная зона непознаваемости уже начинает проявляться в небольших системах, что меняет представления о том, что можно узнать в математике с помощью традиционных средств. BB(6) — это не просто число. Это окно в непостижимую область математических истин, где классическая логика и теоретическая информатика сходятся, чтобы рассказать нам о глубинных границах математического знания.
Прогресс в грузе оценок BB(6) иллюстрирует не только технические новшества, но и эволюцию наших взглядов — от субъективного понимания чисел к новому, более абстрактному осознанию бесконечности и недостижимости полностью формализованных знаний. Таким образом, исследование Busy Beaver 6-го порядка является не только вызовом для современных математиков и логиков, но и маяком, освещающим пути к новым открытиям в понимании природы вычислений, доказательств и математической истины. Чем больше мы узнаём о BB(6), тем яснее становится, насколько сложна и красива вселенная чисел и процессов, спрятанных за каждой простой формулой или определением.