Квазикристаллы — загадочная форма твёрдого вещества, которая десятилетиями ставила в тупик учёных своей необычной структурой и свойствами. Эти материалы занимают промежуточное положение между кристаллами и стеклом, объединяя в себе элементы как упорядоченности, так и хаоса. Недавно команда исследователей из Университета Мичигана совершила значительный прорыв, разработав первое квантово-механическое моделирование квазикристаллов, которое помогло понять, почему они существуют и чем обусловлена их стабильность. Открытие квазикристаллов восходит к 1984 году, когда израильский учёный Даниэль Шехтман обнаружил металлический сплав, атомы которого оказались расположены с пятиосевой симметрией, которая на тот момент считалась невозможной в кристаллах. Квазикристаллы демонстрировали симметрию, которая противоречила традиционному пониманию периодичности кристаллических решёток, что вызвало скептицизм в научном сообществе.
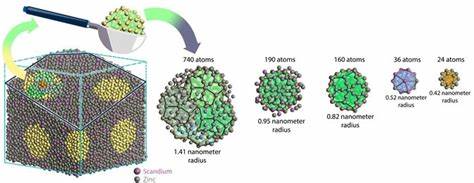
Однако последующие исследования подтвердили существование таких структур в природе и лабораториях, а сам Шехтман получил Нобелевскую премию за это открытие. Главной проблемой, затруднявшей понимание квазикристаллов, была невозможность применять традиционные квантово-механические методы расчёта стабильности кристаллов, такие как теория функционала плотности (DFT). Эти методы основаны на предположении о бесконечно повторяющейся периодичности атомной структуры, что невозможно для квазикристаллов из-за их уникального непериодического упорядочения. Используя инновационный подход, учёные из Университета Мичигана провели моделирование, вырезая маленькие фрагменты квазикристаллов — наночастицы — из большого блока материала. Поскольку в этих наночастицах есть чёткие границы, для них возможно провести квантово-механические расчёты энергии, не требующие бесконечной периодичности.
Моделируя частицы разных размеров, исследователи смогли экстраполировать данные, чтобы понять поведение и стабильность большого масштаба квазикристаллов. Выяснилось, что квазикристаллы являются энтальпийно стабилизированными структурами, то есть они занимают состояние с минимальной энергией, как и обычные кристаллы. Это открытие опровергает предположение, что квазикристаллы существуют лишь благодаря энтропии и хаотическим эффектам, как это происходит в стеклах. Таким образом, квазикристаллы являются основополагающе устойчивыми и фундаментально «правильными» формами материи. Особое внимание в исследовании уделялось двум типам квазикристаллов: сплавам скандия с цинком и иттридия с кадмием.
Новая методика позволила впервые подсчитать их точную квантово-механическую энергию, тем самым подтвердив их термодинамическую стабильность. При этом для масштабирования вычислений учёные разработали усовершенствованный алгоритм, который сокращает время расчётов в сто раз, используя ускорение с помощью графических процессоров и минимизируя коммуникацию между вычислительными ядрами. Полученные результаты важны не только с познавательной точки зрения, но и открывают перспективы для создания новых материалов с заданными свойствами. Понимание того, как именно атомы могут формировать нестандартные упорядоченные структуры без повторения, позволяет материаловедам проектировать квазикристаллические комплексы с уникальными механическими, оптическими и электронными характеристиками. Квазикристаллы уже нашли применение в покрытиях, устойчивых к износу, и в создании новых полупроводниковых материалов.
Более глубокое понимание их квантовой природы может стимулировать развитие нанотехнологий и квантовых вычислений, где сложные атомные структуры играют ключевую роль. Благодаря возможности моделировать стеклообразные, аморфные материалы и интерфейсы кристаллов, новая методика обещает ускорить исследования в области материалов с новыми функциональными возможностями. Таким образом, впервые выполненное квантово-механическое моделирование квазикристаллов не просто закрывает давний пробел в понимании редких материалов, но и указывает на пути создания инновационных технологических решений будущего. Эта работа отражает важность нового взгляда на материю, где правила симметрии и стабильности выходят за рамки классической периодической решётки, открывая дорогу к многообразию ранее недоступных структур.