Современные веб-технологии открывают широкие возможности для создания интерактивных 3D-приложений прямо в браузере, и популярными инструментами для этого являются библиотеки Three.js и Cannon-Es. Первая отвечает за создание и визуализацию трёхмерной графики, вторая — за физическое моделирование объектов, их взаимодействие и реалистичную анимацию. Вместе они подходят для создания различного рода игр, симуляторов и, в частности, 3D-роллеров кубиков, позволяя добиться максимально реалистичного и увлекательного опыта для пользователей. В этом материале расскажем, как шаг за шагом построить надёжный и визуально привлекательный 3D-роллер кубиков на JavaScript без использования текстур и сторонних моделей, применяя программное создание геометрии и физику для имитации броска и определения результата.
Основы создания геометрии кубика начинают с использования Three.js и базовой формы BoxGeometry, представляющей куб. Однако стандартная геометрия слишком грубая для реалистичного воспроизведения кубика, так как у неё острые углы и плоские стороны. В игре с кубиками важна визуальная составляющая – сглаженные округлые углы и углубления на гранях, обозначающие цифры, должны выглядеть плавно и натурально. Один из распространённых подходов — использование RoundedBoxGeometry из примеров Three.
js, который добавляет скругления, но он не даёт полной свободы для реализации выемок и углублений на сторонах кубика. Поэтому оптимальным решением становится создание собственной геометрии путем модификации стандартного куба с большим количеством сегментов. Чтобы добиться эффекта сглаженных углов, необходимо пройтись по каждому вертексу в атрибуте позиции геометрии и внести корректировки в его X, Y и Z координаты. Главная идея — выделить вершины, расположенные возле углов и ребер кубика, и заменить их положения так, чтобы они ложились на поверхность сферы с заданным радиусом скругления. Таким образом задаётся плавный переход между гранями.
Для достижения этого вводится понятие «внутреннего куба» — меньшего куба, ограниченного краями, с которого снимается радиус скругления. Каждая вершина за пределами этого внутреннего диапазона корректируется: те, что находятся в вершинах оригинального куба, смещаются на оборотную сферу; те, что лежат на рёбрах, корректируются соответствующим образом, позволяя сохранить гладкость по всем трем направлениям. Необходимо учитывать нюанс с нормалями – в 3D графике нормали отвечают за правильное освещение поверхностей. После изменения вершин важно пересчитать нормали, чтобы свет правильно отражался от скруглённых граней и углублений. Стандартный метод computeVertexNormals в Three.
js обычно работает, но при дублировании вершин или швов его результаты могут быть неправильными, создавая визуальные артефакты. Для корректной работы требуется удалить дубликаты в геометрии, что решается методом mergeVertices из дополнений Three.js, позволящим объединить повторяющиеся вершины по позиции и перегенерировать нормали для гладкости. Следующий особый элемент дизайна — выемки или «ноты» кубика, имитирующие точки на его сторонах. Чтобы их создать, достаточно выбрать вершины на каждой стороне, определяемые фиксированной координатой (например, по оси Y равной 0.
5 для верхней грани), и сместить их внутрь кубика. Однако форма углублений должна быть плавной, а не резкой, поэтому применяется математическая функция, похожая на косинусный импульс, центрированный по координатам X и Z. В двумерном представлении эта функция строит одиночный гладкий взмах с максимальным значением на центре и затухающий к краям. В пространстве же эффективным решением является умножение двух таких функций по двум осям, создавая плавный и симметричный выемчатый узор на каждой стороне, с возможностью смещения центра углублений для имитации разных расположений точек на кубике. Цветовое оформление кубика остаётся минималистичным и стильным — основную поверхность покрывает светло-серый материал с помощью MeshStandardMaterial трех.
js. Для повышения контраста и усиления визуального эффекта углубления заполняются чёрными плоскостями, размещёнными чуть внутри кубика, чтобы эффективно показывать собой «точки» игрового кубика. Такая конструкция из двух слоёв — внешней поверхности с округлёнными краями и внутренних отверстий — создаёт реалистичный и современный внешний вид, при этом не требует сложных текстур и дополнительных ресурсов. Наступает этап физического моделирования с Cannon-Es — библиотекой, которая обеспечивает симуляцию жёстких тел, столкновений и гравитации. Создаётся физический мир, в котором добавляются объекты: плоскость пола и физические тела кубиков, имитирующие те же размеры, что и визуальные модели.
Важно помнить, что в Cannon-Es при создании Box-формы размер задаётся как половина длины ребра (half extents), что требует аккуратного соответствия с Three.js – там указывается полный размер. Пол в сцене полноценный и статичный объект, полученный и в Three.js (для визуализации), и в Cannon-Es (как тело с типом STATIC). Его позиция и ориентация синхронизируются, чтобы объекты взаимодействовали с ним корректно.
Это фундамент, на который позднее падают кубики. Для анимации применен цикл render, где каждый кадр запускается фиксированный шаг симуляции физического движка. Возвращённые координаты и кватернионы вращения каждого кубика копируются на соответствующие 3D-объекты в Three.js, создавая синхронность между визуализацией и физикой. Такой подход позволяет добиться плавных и реалистичных движений, как будто кубики действительно падают, сталкиваются и останавливаются.
Погружение в детали динамики приводит к добавлению гравитационной силы, которая направлена вертикально вниз и задаёт ускорение для кубиков — в нашей модели значение гравитации превышает земное, но именно экспериментальные настройки помогают добиться игровой выразительности и наглядности, а не точного воспроизведения физических величин. Для повышения реализма вводятся материалы физики и контактные материалы, задающие коэффициенты трения и отдачи (restoration). Повышение значения отдачи приводит к более живой, «отскакивающей» анимации кубиков, которая визуально гораздо более привлекательна и динамична. Чувствительность к физическим свойствам даёт возможность создавать вариации поведения кубиков, экспериментировать с плотностью, массой и другими параметрами. Запуск броска кубиков реализуется через метод, где каждому физическому телу сбрасываются скорость и вращение, затем задаётся стартовая позиция и случайная начальная ротация для создания эффекта непредсказуемого броска.
Важный момент — применение импульса силы, который подталкивает кубики в сторону с некоторым вращением, заданным смещением точки приложения силы от центра масс. Это имитирует настоящий бросок, с вращением и изменением углов падения. Отладка процесса не менее важна: добавляются обработчики событий «сон» для определения момента, когда кубик останавливается. При достижении малых скоростей тело переходит в состояние «усыпления», что сигнализирует о конце броска и позволяет считать результат. Определение результата — это вызов к математике ориентации кубика.
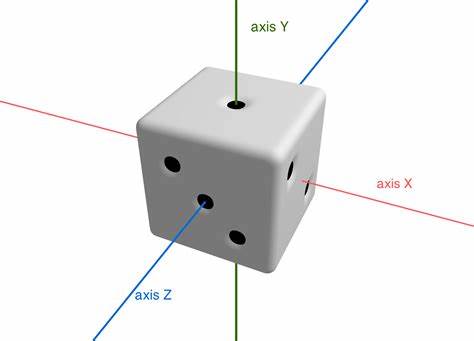
Преобразуя кватернион вращения в эйлеровы углы и анализируя их по определённой схеме выбора, учитывающей порядок вращений YZX и особенности положения сторон кубика, можно однозначно понять, какая грань оказалась сверху. Ключевой аспект — учитывать допустимые погрешности углов, чтобы не засчитать посадку на ребро решением, рассчитать и подождать до полного опускания кубика на грань. В итоге, результаты броска моментально отображаются, создавая интерактивный и разумный игровой опыт, похожий на физический бросок кубиков в реальном мире. Объединение Three.js и Cannon-Es в одном проекте позволяет добиться баланс оптимальной визуализации и сложного физического поведения на стороне клиента без привлечения сторонних движков или дополнительных ресурсов.
Данный подход к созданию 3D-роллера кубиков — отличный пример того, как современные разработки в области фронтенда и Javascript позволяют создавать богатые мультимедийные проекты с полной интерактивностью, которые работают прямо в браузере, не требуя сложной установки и загрузки тяжёлых игр. Такой проект может стать стартовой точкой для образовательных программ, онлайн-игр или элементов интерфейса, требующих моделирование случайных чисел и визуализаций. Множество возможностей остаётся для расширения: добавление пользовательского интерфейса, счётчиков очков, дополнительных эффектов освещения и текстур, поддержка разных видов кубиков или других игральных костей с произвольными формами. Однако базовая база, заложенная при помощи кастомной геометрии, продуманной физической модели и совершенного контроля анимации — это фундамент, на котором можно строить более сложные и визуально насыщенные проекты. Экспериментируя с параметрами скругления углов, формой выемок, значениями силы и материала можно получить бесконечно разные варианты роллера кубиков, что открывает широкое пространство для творчества и оптимизации под нужды конкретной игры или анимации.
Понимание взаимосвязи трёхмерной графики и физического движка чрезвычайно полезно для профессионалов, стремящихся создавать интерактивные приложения на современном стеке технологий. Поэтому освоение этой темы несомненно расширит ваши навыки в области WebGL, 3D программирования и игровой физики, даст опыт работы с современными библиотеками JavaScript и понимание, как тонко настроить поведение визуальных элементов для лучших пользовательских впечатлений. Попробуйте создать собственный 3D роллер кубиков, следуйте логике описанных этапов и не бойтесь экспериментировать — успех не заставит себя ждать.