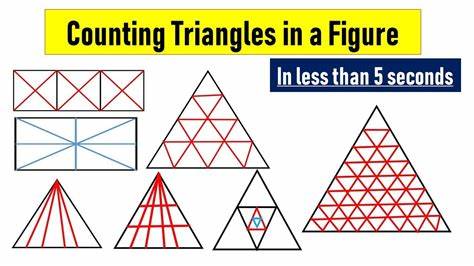
Геометрия давно является неотъемлемой частью математической науки, привлекая внимание как ученых, так и любителей точных наук. Одной из классических задач, которой посвящено множество исследований, является определение максимального количества треугольников, образуемых заданным числом линий на плоскости. В частности, интерес представляет загадка о максимальном количестве треугольников, которые можно получить с помощью 31 прямой. Современные математики и энтузиасты недавно нашли, что 31 линия может образовывать до 299 треугольников, что вызвало большой резонанс среди исследователей комбинаторной геометрии. В данной статье мы подробно разберем, как достигается это число, почему оно является максимальным и какие методы используются в изучении подобных задач.
Задача о максимальном количестве треугольников, образованных линиями, уходит корнями в классическую геометрию. Суть задачи заключается в следующем: если на плоскости задано n прямых, которые пересекаются друг с другом таким образом, чтобы максимизировать количество треугольников, сколько треугольников можно получить? Очевидно, что если линии параллельны либо совпадают, количество образуемых треугольников сокращается. Поэтому для максимизации количества треугольников обычно предполагают, что линии расположены в общем положении, то есть никакие три линии не пересекаются в одной точке, кроме тех, где они встречаются попарно, и никакие две линии не параллельны. Для небольшой величины n простое понимание задачи не вызывает затруднений. Например, с тремя линиями можно получить только один треугольник, с четырьмя – уже четыре, а с пятью – десять.
Однако с увеличением числа линий вычисление максимального количества треугольников становится все более сложным и требует специальных комбинаторных подходов и интуиции. Формулы для общего случая отсутствуют, поскольку конфигурация линий оказывает значительное влияние на результат, а количество вариантов расстановки растет экспоненциально. Ввиду перечисленных сложностей, вниманию математиков представляется задача максимально эффективно располагать линии, чтобы усилить количество треугольников. Известно, что теоретически максимальное количество треугольников, которые можно образовать из n прямых, лежит в диапазоне, обусловленном конечными соотношениями между числом линий и числом их пересечений. Каждая тройка линий, где ни одна не параллельна другой и все пересекаются, образует ровно один треугольник.
Таким образом, максимально возможное количество треугольников ограничено числом комбинаций из трех линий, что равняется сочетанию по формуле C(n, 3). Для 31 линии этот количественный предел можно вычислить как C(31, 3) = 31! / (3! * 28!) = 4495. Однако в практическом расположении линий огромное количество этих треугольников может отсутствовать из-за того, что некоторые линии могут пересекаться в одной точке, или же линия не будет формировать полноценный многоугольник из-за конфигурации других линий. Поэтому достижение этого теоретического максимума невозможно. Иными словами, 4495 – это верхняя теоретическая граница, а неполное количество треугольников возникает при учете геометрических реалий.
Недавнее открытие показывает, что максимально возможное количество треугольников для 31 линии составляет 299. Это число значительно меньше теоретического максимума в 4495, что объясняется сложностью конструкции линий, необходимой для максимального числа треугольников. Речь идет о так называемой оптимальной конфигурации линий, которая обеспечивает наибольшее количество треугольников при конкретном числе линий. При этом оптимальная конфигурация находится за пределами простых применений и требует тщательного проектирования и анализа расположения линий. Фундаментальными инструментами для исследования таких задач выступают методы сочетательной и комбинаторной геометрии.
Сочетательная геометрия изучает структуры пересечений и расположений точек и линий, а комбинаторная геометрия акцентирует внимание на подсчетах и ограничениях, связанных с такими структурами. Благодаря этим методам исследователи выработали ряд теорем, позволяющих предсказывать максимальное число многоугольников, в частности треугольников, создаваемых линиями или отрезками. Одним из ключевых понятий, которое стоит отметить, является так называемая конфигурация «например, без тройных пересечений». Это положение линий, при котором никакие три линии не пересекаются в одной общей точке. Такая конфигурация необходима для получения максимального количества треугольников, поскольку пересечение нескольких линий в одной точке уменьшает общее количество треугольников на плоскости.
Еще одним важным аспектом является врастание связности линии к другим. Формирование треугольника возможно лишь в том случае, если каждые две из трех линий пересекаются, причем созданные точки пересечения находятся в таком расположении, чтобы замыкать фигуру. Благодаря применению анализа взаимных пересечений и принципа оптимальной раскладки достигаются максимумы в количестве треугольников. Практические приложения изучения подобных задач выходят за рамки чисто теоретической геометрии. Такие задачи важны при разработке алгоритмов визуализации данных, компьютерной графики, а также в проектировании различных систем связи и сетей.
Понимание пределов построения сложных конфигураций помогает оптимизировать ресурсы и улучшить эффективность процессов, опирающихся на геометрические структуры. Кроме того, подобные математические открытия вдохновляют ученых и студентов продолжать изучение и расширение знаний в области дискретной математики, выступая в роли примера того, как глубокий математический анализ тесно переплетается с прикладными и теоретическими задачами. Эти знания подтверждают важность базовых понятий геометрии в развитии современных технологий и научных исследований. Подводя итог, можно отметить, что нахождение максимального количества треугольников, образованных 31 линией и соответствующего значению 299, демонстрирует красоту и сложность комбинаторной геометрии. Несмотря на то, что верхняя теоретическая граница гораздо выше, именно такая конфигурация линий является наилучшей с практической точки зрения.
Дальнейшие исследования в этой области продолжаются, что может привести к новым открытиям и улучшениям в понимании структуры многоугольников, их образуемых комбинаций и оптимальных конфигураций линий на плоскости.