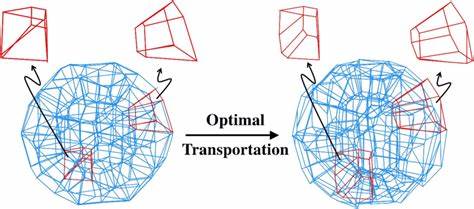
Оптимальный транспорт - это класс математических задач, который ищет наиболее эффективный способ перемещения распределения массы или ресурсов из одного состояния в другое с минимальными затратами. Этот концепт имеет широкое применение в различных научных и инженерных областях, таких как обработка изображений, машинное обучение, экономика и теория вероятностей. Среди разновидностей задач оптимального транспорта особое место занимает полупрерывный или полусдискретный вариант, где одна из мер задана непрерывно, а другая - в виде конечного набора точек с заданной массой. Такой подход позволяет моделировать сложные системы при относительно эффективной вычислительной нагрузке, что критично при работе с большими объёмами данных. Главным вызовом при решении задач семи-дискретного варианта оптимального транспорта становится масштабируемость алгоритмов и их адаптация к большим пространствам данных.
Традиционные методы, которые успешно работают для небольших наборов, зачастую не справляются с объёмами, характерными для современных приложений. Для преодоления этого ограничения активно разрабатываются распределённые алгоритмы, использующие параллельные вычисления и современные структуры данных. Распределённые диаграммы Вороного становятся ключевым инструментом при разделении пространства на регионы, которые удобны для локальных вычислений, существенно ускоряя процесс оптимизации. Диаграммы Вороного - это разбиение пространства на области, каждая из которых относится к ближайшей точке из заданного множества. В задачи полупрерывного оптимального транспорта они внедряются как геометрическая структура, определяющая зоны влияния различных опорных точек распределения.
В классическом варианте диаграммы строятся и обрабатываются в едином вычислительном контексте, что становится проблематичным при больших размерах данных и высокой размерности пространства. Распределённый подход предлагает разделять исходное пространство между вычислительными узлами, каждый из которых строит локальную диаграмму, после чего происходит слияние результатов и корректировка для поддержания глобальных свойств. Современные методы реализуют вычисления через распределённые вычислительные платформы, такие как кластеры и облачные сервисы, тем самым позволяя масштабировать обработку данных на сотни или тысячи ядер процессоров. Важным аспектом становится эффективное управление коммуникацией между узлами и синхронизация данных, чтобы избежать избыточных пересчётов и потерь точности. Алгоритмы, основанные на распределённых диаграммах Вороного, обеспечивают сжатие вычислительных затрат, что открывает новые возможности для применения в задачах мониторинга, плотного моделирования физических процессов, оптимизации логистических сетей и других.
Одним из перспективных направлений является интеграция методов полупрерывного оптимального транспорта с нейронными сетями и глубоким обучением, где распределённые вычисления диаграмм Вороного могут выступать в роли предварительной обработки данных или как часть архитектуры моделей. Такое сочетание позволяет повышать качество выигрыша при работе с большими объёмами разнотипных данных и реализовывать адаптивные модели с учётом геометрических особенностей исходных распределений. В сфере компьютерной графики и анимации использование подобного подхода помогает улучшить алгоритмы обработки текстур и моделирования деформаций. Теоретические исследования подчёркивают важность точной оценки сходимости распределённых алгоритмов и жёстких условий на стабильность построения диаграмм. Кроме этого, критичным моментом остаётся баланс между точностью вычислений и временем отклика системы.
Предложены механизмы динамической адаптации вычислительных ресурсов, что играет большую роль в задачах реального времени и интерактивных системах. Для практического применения разработаны программные комплексы с открытым исходным кодом, что стимулирует дальнейшее развитие сообщества исследователей и специалистов. Значимость применения технологии семи-дискретного оптимального транспорта с распределёнными диаграммами Вороного трудно переоценить в эпоху больших данных и искусственного интеллекта. Они позволяют обрабатывать объёмные и сложные распределения с сохранением вычислительной эффективности и высоким уровнем точности, что способствует прогрессу в фундаментальных науках и промышленности. В будущем ожидается дальнейшее расширение возможностей этих методов за счёт совершенствования архитектур распределённых систем, разработки новых математических моделей и интеграции с другими передовыми технологиями.
Таким образом, полупрерывный оптимальный транспорт с использованием распределённых диаграмм Вороного представляет собой мощный инструмент современного анализа и моделирования, отвечающий на вызовы обработки больших данных и сложных вычислительных задач. Он открывает новые перспективы для исследователей и инженеров, стремящихся к оптимизации процессов в самых разных областях науки и техники. .