Теория узлов – чрезвычайно увлекательная и глубокая область математики, пересекающаяся с топологией, алгеброй и даже физикой. Для исследователей, ученых и любителей в этой сфере очень важен качественный и постоянно обновляемый источник информации, объединяющий классификации, таблицы и инструменты анализа узлов и ссылок. Одним из таких ресурсов является Атлас узлов (The Knot Atlas) – интерактивный и открытый проект, собирающий самые актуальные данные по теории узлов и отражающий дух коллективного сотрудничества, характерного для вики-платформ. Атлас узлов представляет собой уникальную платформу, на которой любой желающий может найти подробную структурированную информацию о различных типах узлов и ссылок, их классификациях и свойствах. Созданный и развиваемый главными авторами Скоттом и Дрором, проект открыт для участия сообществу, что обеспечивает постоянное пополнение и корректировку данных.
Это особенно важно для такой динамичной области, где появляются новые исследования и результаты. Одной из ключевых составляющих Атласа является набор таблиц, в которых систематизированы узлы по числу перекрестков и другим характеристикам. Например, таблица Рольфсена содержит классификацию узлов с числом перекрестков до десяти; таблица Хоста-Тислтуэйта включает узлы с одиннадцатью перекрестками; есть также таблица Тислтуэйта для ссылок, а также особый каталог торических узлов с числом перекрестков до 36. Наличие таких таблиц позволяет легко ориентироваться как начинающим, так и опытным исследователям, искать нужные объекты и анализировать их свойства. Кроме того, Атлас содержит интеграцию с мощным пакетом Mathematica – KnotTheory`, который предоставляет инструменты для математического анализа и визуализации узлов.
Этот пакет широко используется специалистами для проведения вычислений, моделирования и проверки гипотез, что значительно расширяет возможности пользователей Атласа. Большое значение в проекте уделяется взаимодействию пользователей и развитию сообщества. Благодаря особенностям вики-структуры платформы, любой зарегистрированный пользователь способен редактировать и добавлять информацию почти в любой раздел. Подобный подход способствовал созданию богатой и достоверной базы данных, которая постоянно расширяется и обновляется. Важная часть работы – это список задач, где обозначены направления и планы по дополнению и совершенствованию ресурса.
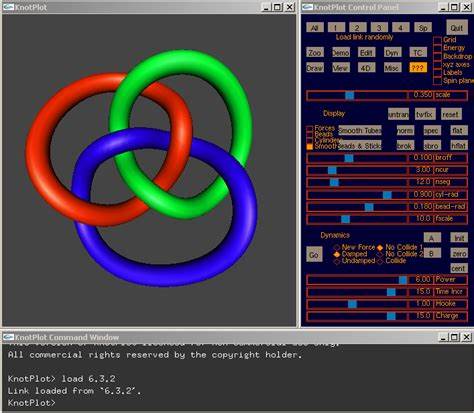
Ещё одной интересной особенностью Атласа являются дополнительные материалы и инструменты, которые включают в себя построение трехмерных визуализаций узлов с помощью программы TubePlot, удобный интерфейс WikiLink для взаимодействия с MediaWiki, а также коллекцию виртуальных и рациональных узлов, представленных в таблицах и базах данных. Эти ресурсы помогают глубже понять структуру и взаимосвязи узлов, а также служат наглядным пособием для обучения и исследовательской работы. Важно отметить, что Атлас узлов тесно связан и с другими выдающимися математическими ресурсами, которые служат важным подспорьем в изучении теории узлов. Среди них выделяются таблицы Джереми Грина по виртуальным узлам, база данных KnotInfo Чака Ливингстона, атлас рациональных узлов Германа Грубера, а также онлайн-инструменты Линка Knot и база данных виртуальных ссылок от Пола Цинн-Джастина, а также вебматематические решения от Славика Яблана и Радмилы Сазданович. Эти ссылки делают Атлас узлов частью глобального образовательного и научного пространства в топологии.
Необходимо также подчеркнуть философскую и культурную значимость темы. Известная цитата, слегка измененная, принадлежит математику Леопольду Кронекеру: «Бог создал узлы, все остальное в топологии — дело смертных». Она подчеркивает важность узлов как фундаментального объекта изучения, а Атлас в этом контексте выступает как современный инструмент постижения этой божественной тайны. А для широкой аудитории цитаты из литературы, например Лемони Сникета, оживляют восприятие темы, напоминая о красоте и сложности узлов в повседневной жизни и искусстве. Для тех, кто решится погрузиться в изучение теории узлов и воспользуется Атласом, открывается богатейший мир математических объектов с множеством приложений — от теоретической физики до компьютерной графики и биологии.