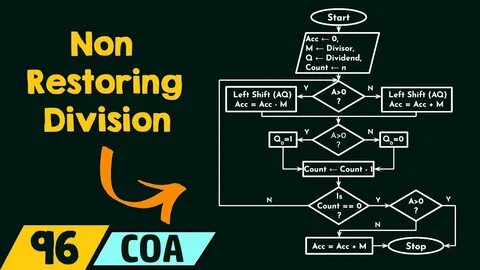
Алгоритм деления без восстановления занимает важное место в области компьютерной арифметики и цифровой логики. Он широко применяется в процессорах и специализированных вычислительных устройствах благодаря своей эффективности и возможности упрощения аппаратной реализации. Однако при изучении и внедрении данного алгоритма у многих разработчиков и студентов возникают вопросы и сложности, связанные с его пониманием и практическим применением. В этом материале мы подробно разберём суть алгоритма, особенности его работы, типичные ошибки и способы их преодоления, что позволит избавить вас от неуверенности и сомнений при использовании этой техники деления. Прежде чем погружаться в детали алгоритма, полезно вспомнить суть задачи деления.
Деление представляет собой операцию нахождения частного и остатка от деления одного числа на другое. В цифровой электронике и программировании эта процедура реализуется с помощью ряда итеративных вычислений, которые должны быть быстрыми и устойчивыми к ошибкам. Алгоритм деления без восстановления - один из классических способов выполнения этой операции, который оптимизирует некоторые этапы и избавляется от необходимости повторных корректировок в процессе вычислений. Основная идея деления без восстановления основана на последовательных сдвигах и вычитаниях с условным добавлением делителя, чтобы корректировать оценки частного и остатка. В отличие от алгоритма с восстановлением, где при отрицательном остатке после вычитания делителя происходит дополнительное сложение для "восстановления" значения, здесь происходит другая логика обработки результата.
Это позволяет сэкономить аппаратные ресурсы и уменьшить время выполнения операции, поскольку не требуется возвращать промежуточные значения обратно при обнаружении несовпадений. Для понимания алгоритма необходимо рассмотреть процедуру пошаговых итераций. На каждой итерации рассматривается частично вычисленное значение и исходные данные - делимое и делитель. В процессе сдвигов происходит последовательное вычитание или сложение с делителем в зависимости от знака промежуточных результатов. Частное формируется из знаков результатов каждой итерации.
Это требует аккуратного отслеживания знаков чисел и правильной организации хранения промежуточных результатов. Одним из частых вопросов является обработка отрицательных значений при выполнении вычитаний и сложений. В цифровой арифметике это обычно реализуется при помощи дополнительного кода, который позволяет выполнять операции с отрицательными числами без специальной обработки знака. Однако это накладывает определённые требования на реализацию алгоритма и разбиение битовых полей для частного и остатка. Неправильное управление знаками или неверное использование дополнительного кода часто становится источником трудностей для разработчиков.
Другой сложный момент - окончательная корректировка результата по завершении итераций. В стандартном алгоритме с восстановлением после основной серии операций проводится этап проверки и корректировки остатка и частного для соответствия математическим определениям деления с остатком. В алгоритме без восстановления такая дополнительная корректировка отсутствует или существенно упрощена, однако это требует тщательного контроля и правильного выбора шагов во время итераций. Ошибки на этом этапе могут привести к некорректным результатам деления, что особенно критично в вычислительных системах с требованиями к точности. Практическая реализация алгоритма нередко вызывает вопросы, связанные с выбором формата хранения чисел и разрядности регистров.
Для деления целых чисел применяется обычно операции с фиксированным количеством бит, что накладывает ограничения на максимально допустимые значения делимого и делителя. Применение алгоритма к числам в формате с плавающей запятой требует дополнительной подготовки данных и преобразований, что усложняет реализацию. Важно учитывать специфику аппаратной платформы и возможности языка программирования или микроконтроллера при выборе метода реализации. Кроме того, для повышения надежности и производительности алгоритма часто совмещают его с защитой от переполнения и другими методами корректировки ошибок. Это сопряжено с дополнительными вычислительными затратами, но существенно увеличивает точность и качество результата.
Например, использование дополнительных регистров для хранения промежуточных значений и контрольных сумм позволяет избежать пропуска ошибок в вычислениях. На практике при изучении алгоритма деления без восстановления важно проводить поэтапный разбор каждого шага и реализовывать тестовые примеры с понятным промежуточным результатом. Обсуждение частых ошибок и неочевидных нюансов позволяет лучше понять логику работы алгоритма и усвоить механизмы коррекции. Особенно полезно сравнение с алгоритмом с восстановлением, демонстрирующее преимущества и недостатки обеих техник. Также стоит обратить внимание на существующие реализации алгоритма в различных языках программирования и аппаратных описательных языках.
Анализ готовых решений снижает вероятность ошибок и ускоряет процесс внедрения. Комментарии к коду и пошаговые пояснения позволяют быстрее адаптировать алгоритм под конкретные задачи и интегрировать в более сложные вычислительные системы. В контексте развития современных компьютерных архитектур алгоритм деления без восстановления продолжает оставаться актуальным, поскольку обеспечивает баланс между простой аппаратной реализацией и необходимой точностью вычислений. Несмотря на появление более сложных методов и специально оптимизированных инструкций в современных процессорах, понимание классических алгоритмов помогает инженерам глубже осознавать принципы работы вычислительных устройств и создавать собственные решения, адаптированные под уникальные задачные критерии. Подводя итог, можно сказать, что алгоритм деления без восстановления - это эффективный и экономичный метод выполнения операции деления на цифровых устройствах.
Несмотря на кажущуюся сложность логики, правильное изучение и практическое применение этого алгоритма открывает возможности для создания надежных и быстрых вычислительных систем. Внимательное отношение к деталям, понимание особенностей работы со знаковыми числами и тщательное тестирование помогут вам успешно справиться с возникающими трудностями и использовать алгоритм в своих проектах. В итоге, владение техникой деления без восстановления станет важным преимуществом для инженеров и разработчиков, работающих в области цифровой электроники и программирования. .