Числа Коллатца давно привлекают внимание ученых и энтузиастов математики благодаря своей простоте определения и при этом загадочной динамике. Обозначая функцию Коллатца как f(n), которая принимает значение n/2, если n четно, и 3n+1, если n нечетно, исследователи пытались найти закономерности в поведении чисел, проходящих через эту функцию, до тех пор, пока не достигают конечного состояния при n=1. Одним из интересных подходов, позволяющих глубже понять структуру этих чисел, стала классификация по восьми различным классам на основе взаимодействия функции и некоторого абстрактного устройства – «ленты», где запись состояния осуществлялась человечески необычным образом. Представим ленту с неограниченным числом ячеек, сначала все пустых и неактивных, и магнитофонную головку, расположенную в центральной позиции. Головка перемещается по ленте, применяя правила Коллатца к стартовому числу n, при этом изменяя состояние яечек: при четном n выполняется переход вправо, при нечетном – влево, а текущее клеточное состояние инвертируется, то есть меняется с 0 на 1 или наоборот.
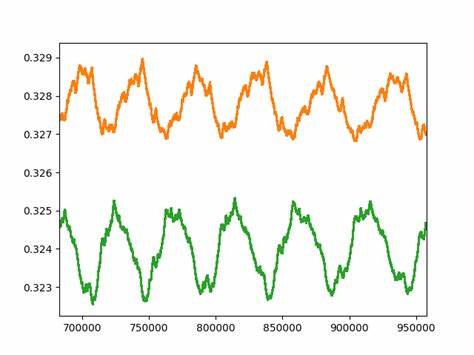
Это создает уникальный паттерн за период итераций, которые заканчиваются при достижении n=1. Таким образом, каждая последовательность имеет определённое количество отмеченных ячеек – сумма, и длину остановки – время, а также распределение отмеченных клеток относительно посещенных. Для примера рассмотрим число 27, одно из самых известных с длительной последовательностью в загадочной проблеме Коллатца. Для него характеризуется длина остановки τ=111, а на последнем шаге располагается 13 отмеченных клеток. Изображение состояния ленты можно сжать до компактной записи, напоминающей строку, в которой отражены ключевые моменты паттерна ячеек.
Отношение числа отмеченных клеток к общему числу посещенных (это называют ratio T/1space(n)) дает представление о способности числа «записать» и поддерживать состояние посещенных ячеек на ленте. Интересным фактом является то, что среди этих отношений существует всего четыре основных диапазона значений, разбитых дополнительно на два подкласса, что дает в сумме восемь категорий. Эти классы имеют следующие интервалы и частоты встречаемости: к первым относятся значения в диапазоне от 0 до 0.005 и 0.005 до 0.
01, средние классы охватывают промежутки от 0.09 до 0.095 и 0.095 до 0.1, а высокие достигают от 0.
9 до 0.905, 0.905 до 0.91, 0.99 до 0.
995 и, наконец, 0.995 до 1. Последний интервал особенный – он включает степени двойки, которые всегда движутся вправо по ленте, заполняя ячейки до остановки последовательности. Анализ распределения чисел в каждом классе между 2 и 100 показал довольно интересное распределение. Например, первый класс содержит числа как 11, 26 и 47, второй – 10, 27, 42, четвертый класс включает 3, 15, 18, а восьмой – 2, 4, 6, 8 и так далее.
Таким образом, по набору параметров можно четко понять, к какому классу принадлежит число, и, следовательно, получить представление о дальнейшем развитии его последовательности на ленте. Зачем нужна такая классификация? В первую очередь, она помогает углубить понимание динамических систем и закономерностей, которые скрываются за кажущейся хаотичностью функции Коллатца. Интерес к этим числам обусловлен тем, что, несмотря на свой долгий срок существования, пока не удается доказать гипотезу Коллатца, которая утверждает, что всякая последовательность докажет достижение точки 1. Разбиение на классы по отношению ratio T/1space(n) помогает уловить скрытые шаблоны и, возможно, отобразить взаимосвязи между структурой последовательности и поведением на сингулярном уровне. Высокие значения ratio показывают, что число эффективно зафиксировало посещение ячейки, поддерживая отметку в процессе итераций, а низкие – свидетельствуют о том, что число чаще меняло состояние ячеек, оставляя меньше постоянных отметок.
По своим свойствам, классы можно рассматривать как своего рода «характерную подпись» числа в рамках механизма Коллатца, что открывает новые перспективы для прогнозирования поведения или даже выделения подмножеств чисел с общими признаками. Например, степени двойки, принадлежащие самому высокому классу, могут служить примером самых предсказуемых и «прямых» траекторий. Однако сама природа распределения чисел по этим классам вызывает вопросы. Почему некоторые классы встречаются вдвое чаще, чем другие? Ответ частично связывают с методом сжатия дорожки записи ленты и интерпретацией состояния, но полностью эта загадка остаётся открытой. Возможно, за ней стоят глубинные симметрии и теоретические принципы, ещё не изученные в деталях.
Пытаться вывести простые формулы или характеристики чисел, относящихся к каждому классу, становится сложнее, поскольку наборы распределения включают разрозненные по своей цифровой структуре значения. Однако наблюдения показывают устойчивые общие черты, указывающие на то, что некие алгоритмические свойства или степень «хитрости» числа при движении по функции Коллатца влияют на его положение в данной классификации. Важной составляющей анализа становится визуализация распределений — от плотно заполненных гистограмм до цветовых карт по отношению к жизненному циклу числа в Collatz-последовательности. Эти инструменты позволяют интуитивно осмыслить, как именно эти 8 классов формируются и какие закономерности проявляются при увеличении размеров исследуемых чисел. Границы классов, наблюдаемые при увеличении выборки до n=10^6, сохраняют свою актуальность, что подтверждает устойчивость классификации.