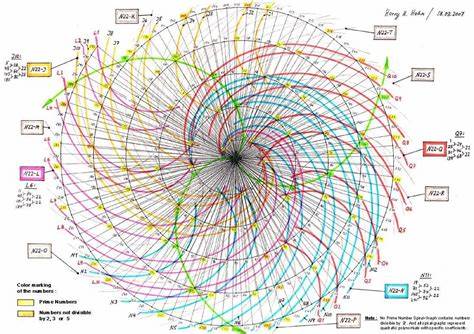
Распределение простых чисел всегда привлекало внимание как математиков, так и ученых из других дисциплин благодаря своей необычайной загадочности и глубоким свойствам. Прямые закономерности расположения простых чисел сложно проследить, а традиционные аналитические методы иногда оказываются затруднены в ответах на основные вопросы. Именно поэтому появился интерес к изучению простых чисел в новой плоскости — с помощью геометрических моделей и визуализаций, что позволяет воспринимать порядок и хаос в их распределении глазами и интуицией, выходя за пределы классических формул и теорем. Одним из ярких примеров такого подхода является идея, получившая название Jacob’s Ladder — своеобразная "лестница Иакова", представляющая последовательность чисел на двумерном графике. Здесь каждое число наносится на ось абсцисс, а ординатой служит позиция, которая меняется в зависимости от простой ли это число.
Если число простое, график меняет направление — поднимается вверх или опускается вниз, создавая зигзагообразный узор, напоминающий лестницу. Для начальной точки 1 график стартует на нуле — уровне моря, затем простой номер 2 заставляет траекторию пойти вниз, следующий простой номер 3 меняет направление движения вверх, а непростые числа не вносят изменения, продолжая движение по выбранному направлению. Эта простая визуализация создает картину мира, где "горы" и "глубины" символизируют серии чисел, отражая их упорядоченность и пропуски по цепочке простых. Морской уровень — ось, равная нулю, выступает в роли границы между "сушей" и "водой" данного математического ландшафта. При расширении графика от единицы и дальше, становится очевидным, что "лестница" простирается все дальше, и расстояния между простыми могут вызывать внезапные резкие изменения графика, что свидетельствует о том, что разрывы между простыми числами могут становиться бесконечно большими.
Эта величина разрывов порождает интересные вопросы: существуют ли "навечно" непосещаемые точки на этой координатной плоскости? Будут ли положительные и отрицательные значения графика встречаться с одинаковой частотой, то есть существуют ли равные объемы "гор" и "морей" при бесконечном продолжении? Эти вопросы — далеко не тривиальны. Несмотря на простоту определения алгоритма, который управляет лестницей, их ответы находятся в области нерешенных проблем современной математики. Процесс может рассматриваться как своеобразное случайное блуждание, но с детерминированными параметрами, зависящими от арифметических свойств простых чисел. Другое перспективное направление исследований основывается на концепции так называемого "prime walk" (прайм-уок), который интерпретирует последовательность простых чисел как маршрут на двумерной сетке. Каждое последующее простое число (за исключением 2 и 5) задает направление движения в зависимости от своей последней цифры: если номер заканчивается на 1 — шаг вниз, на 3 — вверх, 7 направо, 9 налево.
Таким образом создается сложный путь, контролируемый десятками тысяч простых чисел, размещаясь на плоскости, формируя узоры и исследуя геометрию процесса более глубоко. Первые исследования prime walk породили множество интересных гипотез. Главным из них был вопрос, способен ли этот путь покрыть всю бесконечную плоскость или существует ограничение, после которого он перестанет расширяться в определенных направлениях. Исходная догадка предполагала, что область покрытия будет неограничена. Позже, после детального математического анализа и упорных исследований, гипотеза была подтверждена — путешествие продолжится бесконечно, охватывая все новые и новые области плоскости.
Однако в области, исследованной этим маршрутом, остаются немногие точки, которые, возможно, не будут посещены ни единожды. Это вызывает новые препятствия и открытые вопросы: какие свойства определяют доступность тех или иных точек? Есть ли "запретные области" для prime walk? Эти вопросы сложны не только с технической стороны, но имеют глубокое философское значение, ведь они касаются распределения числовых структур и природы случайности внутри числовых закономерностей. Отрисовка и визуальный анализ подобных алгоритмов оказываются не только полезными инструментами для постижения абстрактных свойств простых чисел, но и мостом между теорией чисел, комбинаторикой и компьютерной наукой. Они открывают путь к изучению случайных блужданий, связанного с теорией вероятностей, и влияют на понимание теории алгоритмов и вычислимости. Непосредственный контакт с графическим представлением стимулирует появление новых гипотез, что в конечном итоге ведет к открытию новых связей и перспектив в исследовании древней математической темы.
Кроме того, такой геометрический разбор простых чисел служит отличным примером междисциплинарного подхода, объединяющего математику, информатику и даже философию. Исследования показывают, что несмотря на детерминированную природу простых чисел и строгие правила генерации путей, в этих системах возникает удивительный уровень сложности и структурированного хаоса. Важный аспект, который стоит отметить, — это открытость вопросов, поставленных в данных исследованиях. Так называемая «бесконечная нулевая гипотеза» в Jacob’s Ladder ставит задачу выяснить, будет ли в бесконечной перспективе количество пересечений «уровня моря» равным с положительной и с отрицательной стороны. Несмотря на простоту формулировки, ответ изначально казался недоступным, что стимулировало интерес ученых к дальнейшим изысканиям.
Подобные задачи являются прекрасным примером того, что сложные вопросы иногда сокрыты за кажущейся простотой и тривиальностью. Интересен также аспект, который затрагивает метаматематику и теорию вычислимости: существует ли связь между бесконечными путями, построенными на простых числах, и всевозможными алгоритмами, представленными в форме Машины Тьюринга? Этот взгляд наталкивает на размышления о том, можно ли считать такие пути носителями или репрезентантами широкого спектра вычислительных процессов. Возможно, существует фундаментальная взаимосвязь, которую стоит исследовать для понимания границ алгоритмической сложности и вероятностных моделей. Таким образом, подход, основанный на геометрической интерпретации распределения простых чисел, не только расширяет инструментарий для приближения к классическим проблемам теории чисел, но и порождает новые, свежие вопросы и методики. Визуализации и моделирование в виде случайных блужданий и зигзагообразных графиков открывают уникальную возможность для исследователей и любителей математики глубже погрузиться в загадочный мир простых чисел, увидев их в новом, неожиданном свете.
В перспективе именно развитие таких креативных методов может привести к прорывам в доказательстве фундаментальных гипотез, созданию более эффективных алгоритмов для поиска простых чисел и расширению наших теоретических представлений о природе числовых последовательностей. В конце концов, объединение визуального восприятия и математической строгости может воплотиться в мощном инструменте для решения одних из самых древних и интригующих задач человеческой науки.