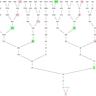
Гипотеза Коллатца — одна из самых интригующих и загадочных математических задач, которая заинтересовала как ученых, так и программистов по всему миру. Эта проблема, впервые предложенная немецким математиком Лотаром Коллатцем в 1937 году, формулируется довольно просто, но до сих пор не имеет доказаного решения. Суть гипотезы состоит в том, что любо́е положительное целое число, при последовательном применении определенного преобразования, в конечном итоге приводит к числу 1. Алгоритм преобразования Число, с которого начинается процесс, определяет всю последовательность. Правила преобразования просты: если число четное, его делят на два.
Если нечетное — умножают на три и прибавляют один. Этот цикл повторяется, пока число не достигнет единицы. Несмотря на свою простоту, гипотеза остается неподтвержденной, и именно поэтому она стала предметом активных исследований в математике и информатике. Реализация алгоритма на языке Scheme представляет собой элегантный пример функционального подхода к программированию. Scheme, являясь одним из диалектов Lisp, отличается минималистичным синтаксисом и мощными возможностями для работы с рекурсией и списками, что идеально подходит для выражения таких математических операций.
Основой реализации для гипотезы Коллатца на Scheme является рекурсивная функция, которая на каждом шаге обрабатывает текущее число в соответствии с правилами преобразования и вызывает себя с новым значением. Пример такой функции можно представить следующим образом: если число равно единице, возвращается результат, завершение рекурсии. Если же оно четное — функция вызывает себя с аргументом, равным половине текущего числа. В случае нечетного числа происходит умножение на три с прибавлением единицы, после чего рекурсия продолжается с новым значением. Данный подход позволяет не только проверить конечность последовательности для конкретного числа, но и проследить весь путь преобразований, сохраняя или отображая промежуточные значения.
Важно отметить, что использование Scheme для такой задачи демонстрирует гибкость и выразительность функционального программирования, давая возможность лаконично и эффективно описывать алгоритмы, связанные с рекурсией и обработкой числовых последовательностей. В более расширенных версиях программы можно добавить счетчик итераций, который фиксирует количество применений преобразования до достижения числа 1. Такая метрика ценна для анализа сложности последовательностей, выявления закономерностей и исследования распределения длины траекторий для различных начальных значений. Данные, полученные таким образом, могут быть визуализированы для более наглядного понимания поведения функции Коллатца, например в виде графиков, где ось Х соответствует исходным числам, а ось У — количеству итераций. Интересно отметить, что доказательство гипотезы Коллатца остаётся открытой задачей в современной математике.
Несмотря на то, что компьютерные проверки охватывают огромный диапазон чисел и подтверждают вывод о достижении единицы, формального доказательства, применимого ко всем натуральным числам, пока не найдено. Это делает изучение и реализацию гипотезы особенно привлекательной областью для энтузиастов программирования и исследователей, которые могут экспериментировать с различными подходами и анализировать динамические свойства последовательностей. Кроме того, реализация на Scheme может стать отправной точкой для создания более сложных моделей и симуляций, включающих оптимизации и улучшения. Например, применяя мемоизацию, можно значительно уменьшить время вычислений, запоминая уже обработанные значения и их соответствующее количество шагов до единицы. Такие техники подчеркивают важность комбинирования теоретической математики с практическими аспектами программирования.
Гипотеза Коллатца и ее применение в Scheme не ограничиваются преподаванием или учебными проектами. Они находят отклик в задачах, связанных с теорией чисел, криптографией, а также в исследовании хаотических систем и динамических процессов. Возможности языка Scheme, особенно в части чистоты выражения идей и поддержки рекурсии, делают его ценным инструментом для подобных задач. В заключение, реализация гипотезы Коллатца на языке Scheme — это не просто техническое упражнение, а окно в мир глубокой математической загадки и мощных вычислительных paradigms. Этот проект объединяет исторический контекст, современные программные технологии и философию функционального программирования, предлагая как новичкам, так и опытным разработчикам увлекательное и познавательное путешествие в область числовых последовательностей и алгоритмов.
Такие реализации помогают лучше понять структуру задач, стимулируют творческое мышление и развивают навыки решения проблем на стыке математики и информатики.