Теорема Гёделя о неполноте: фундаментальные ограничения формальных систем

Биткойн

Теорема Гёделя о неполноте — одно из самых значимых открытий в математической логике XX века, оказывающее глубокое влияние не только на математику, но и на философию, информатику, теорию познания. Формулированная куртом Гёделем в 1931 году, она кардинально изменила представления о семействах формальных аксиоматических систем и о возможностях их исчерпывающего описания. Понимание сути и масштабов этой теоремы важно для тех, кто интересуется фундаментальными вопросами математики и природы формального мышления, а также для разработчиков алгоритмов и искусственного интеллекта. Для того чтобы полностью осмыслить суть теоремы, нужно вернуться к истокам формальных систем. Формальные системы — это строго определённые совокупности аксиом и правил вывода, позволяющие формализовать различные области математики.

Традиционная задача, стоявшая перед учёными в начале XX века, заключалась в том, чтобы представить все математические истины в форме исчерпывающей, последовательной и алгоритмически проверяемой системы аксиом. Цель состояла в создании универсальной «машины» для доказательства любых математических утверждений, исключающей ошибки и противоречия. Однако эта идея была подорвана благодаря работам Гёделя. Он показал, что в любой достаточно мощной формальной системе, которая способна описывать арифметику натуральных чисел и которая при этом является последовательной (то есть в системе нельзя доказать одновременно утверждение и его отрицание), всегда существуют такие истинные утверждения, которые невозможно ни доказать, ни опровергнуть внутри этой системы. Иными словами, никакая система не может быть одновременно полной и последовательной.

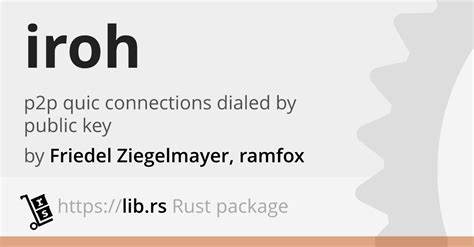
Гёдель формализовал этот результат с помощью построения формулы, которая фактически утверждает о собственной непривязке к доказательству в рамках данной системы. Эта ситуация напоминает парадокс «Это утверждение ложно», но всё же остаётся логически корректной и конструктивной формулой. Доказательство Гёделя использовало методы кодирования математических утверждений и доказательств в виде чисел, что позволило формализовать понятие «доказуемости» и применить формальные логические рассуждения к самой системе. Этот фундаментальный результат продемонстрировал, что формальные аксиоматические системы, такие как теория Пеано для арифметики, не в состоянии полностью охватить всю полноту математической истины посредством собственных аксиом и правил вывода. Подобные ограничения означают, что человечеству необходимо либо принять невозможность построения общей универсальной системы, либо искать другие пути развития математики и формальной логики.

Кроме того, теорема Гёделя приобрела большое и даже спорное значение в философских дискуссиях о природе человеческого разума и сознания. Некоторые исследователи интерпретировали её как доказательство невозможности моделирования человеческого мышления с помощью алгоритмов, то есть машин. Аргумент заключается в том, что если система, основанная на алгоритмах, всегда будет неполной, то человеческий разум каким-то образом превосходит алгоритмические возможности. Однако данная интерпретация нередко подвергается критике. Многие учёные отмечают, что теорема не утверждает невозможность нахождения истин и доказательств с помощью алгоритмов, а лишь устанавливает принципиальные ограничения для формальных систем, построенных на аксиомах и логических правилах.

Более того, человеческие процессы доказательства зачастую можно рассматривать как сложные алгоритмы, а интеллектуальная интуиция и творческий подход не сводятся исключительно к механике вывода теорем. С точки зрения информатики теорема Гёделя связана с фундаментальными вопросами о вычислимости и алгоритмической разрешимости задач. Существует прямая связь с теоремой Тьюринга о неразрешимости проблемы останова, которая показывает, что не существует универсального алгоритма, способного для произвольной программы определить, завершится ли её выполнение. Это также отражает базовые ограничения, связанные с формальной системой и алгоритмами. В современной математике осознание ограничений формализма стимулирует развитие альтернативных подходов к доказательствам и исследованиям.

Среди таких направлений можно отметить неаксиоматические методы, эвристические и вероятностные рассуждения, а также применение компьютерных доказательств, которые хоть и основаны на алгоритмах, способны облегчать работу математики за счёт вычислительной мощности. Теорема Гёделя остаётся предметом активного изучения и дискуссий. Различные области науки продолжают исследовать её последствия для логики, философии, теории информации и искусственного интеллекта. В философии она затрагивает вопросы о природе истины и познания, в логике — границы формализации, в информатике — возможности автоматизации мышления, а в математике — фундаментальные структуры самой науки. Подводя итог, можно сказать, что теорема Гёделя о неполноте — не просто технический результат в математике, а глубокое открытие, изменившее понимание того, что значит доказать истину.

Она демонстрирует, что любые попытки построить совершенную систему знаний сталкиваются с обязательными ограничениями, заставляя человечество постоянно искать новые пути познания и развития. В этом смысле теорема не ограничивает, а, наоборот, расширяет горизонты научной мысли, открывая пространство для творчества и философских поисков. Её изучение важно для всех, кто стремится понять природу математики, логику человеческого разума и границы формальных систем.