Современные вычислительные задачи в областях физики, инженерии и химии нередко связаны с обработкой огромных массивов данных, требующих оценки взаимодействий между множеством частиц или элементов. Одним из самых эффективных и революционных методов решения таких задач стал быстрый мультипольный метод (БММ, англ. Fast Multipole Method, FMM). Этот инновационный алгоритм значительно ускоряет расчёт долгосрочных сил взаимодействия в n-тельных задачах, снижая вычислительную сложность и потребление памяти, что делает его незаменимым инструментом для учёных и инженеров по всему миру. В данной статье подробно рассмотрены основные концепции, применение и преимущества быстрого мультипольного метода, раскрываются его принципы и основные этапы, а также поясняется, почему он был признан одним из важнейших алгоритмов XX века.
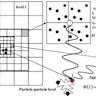
Исторический фон и суть метода Быстрый мультипольный метод был разработан в 1980-х годах Лесли Грингардом и Владимиром Рохлиным младшим. Он возник как ответ на классическую проблему n-тел, в которой необходимо вычислить взаимодействия между большим количеством частиц, например гравитационных или электростатических сил. Традиционный подход, предусматривающий прямое вычисление парных взаимодействий, обладает квадратичной вычислительной сложностью O(N²), что резко ограничивает масштаб решаемых задач. БММ же трансформировал эту задачу, используя математический приём мультипольного разложения. Ключевая идея заключается в том, что источники, расположенные близко друг к другу, могут быть объединены и аппроксимированы как единый мультипольный источник при рассмотрении их взаимодействия с удалёнными точками.
Для этого используется так называемая мультипольная экспансия, основанная на разложении функций Грина, что позволяет свести огромное число взаимодействий к более компактной форме. Затем эта компактная информация эффективно переиспользуется, тем самым существенно снижая количество необходимых вычислений. Как работает быстрый мультипольный метод Принцип работы БММ можно объяснить на примере одномерной задачи: необходимо вычислить сумму от всех источников с определёнными весами в каждой интересующей точке. При прямом подходе число операций равно произведению числа источников и числа точек, что при больших данных становится непрактичным. Быстрый мультипольный метод решает эту проблему с помощью интерполяции полиномиальными базисами Чебышева в так называемых «локальных разложениях».
Если источник и точка достаточно удалены, функция взаимодействия может быть приближена полиномом, что позволяет выполнить расчёт с гораздо меньшим числом операций. Для достижения максимальной эффективности область вычислений рекурсивно делится на иерархические уровни, в каждом из которых взаимодействия между удалёнными группами источников обрабатываются через мультипольные и локальные разложения. Это гарантирует, что число источников в каждой ячейке ограничено, а вычисления между ячейками осуществляются только в тех случаях, когда расстояние между ними превышает определённый порог. Таким образом, общий объём работы сокращается с квадратичного до почти линейного уровня с небольшой логарифмической поправкой, связанной с точностью вычислений. Преимущества применения БММ Использование быстрого мультипольного метода имеет множество значимых преимуществ.
Первое и главное — это драматическое сокращение вычислительных затрат. Переход от O(N²) к O(N log(1/ε)), где ε — заданная точность, позволяет обрабатывать значительно большие задачи без затрат на высокопроизводительные вычислительные мощности. Кроме того, БММ снижает требования к памяти, так как для матричных операций, характерных для задач многих физических систем, не требуется сохранять все элементы во внутренней памяти. Это особенно важно при работе с методами моментa и метода граничных элементов, где исходные матрицы могут быть очень плотными и ёмкими. Вычислительная точность также поддерживается на высоком уровне, благодаря контролируемой ошибке аппроксимации, что особенно ценно в научных приложениях, где малейшие погрешности могут приводить к неправильным результатам.
Области применения Быстрый мультипольный метод нашёл применение в различных областях науки и техники. В вычислительной электромагнетике он активно используется для ускорения итеративных методов решения уравнений Максвелла и в расчетах по методу моментов, что позволяет эффективно моделировать сложные антенные системы, электромагнитное рассеяние и биомедицинские задачи. В квантовой химии БММ применяется при расчёте кулоновских взаимодействий в методах Хартри–Фока и теории функционала плотности, обеспечивая линейное масштабирование вычислений на больших молекулах. Это открывает новые возможности для исследования сложных молекулярных систем и материалов. Также метод широко используется в задачах астрофизики, например при моделировании гравитационного взаимодействия в звёздных скоплениях, и в вычислительной механике для решения задач потенциалов, упругости и гидродинамики.
Современные реализации и программные решения Благодаря популярности и значимости быстрого мультипольного метода, существует множество его реализаций в виде открытого и коммерческого программного обеспечения. Современные библиотеки ориентированы на параллельные вычисления с использованием многопоточных процессоров и графических ускорителей, что позволяет эффективно масштабировать вычисления на суперкомпьютерах. Некоторые из известных реализаций включают программы Puma-EM для работы с методом моментов и мультиуровневым БММ в электромагнитике, а также специализированные библиотеки KIFMM3d и PVFMM для трёхмерных задач. Эти инструменты открывают доступ к мощным методам широкому кругу исследователей и инженеров. Заключение Быстрый мультипольный метод представляет собой один из наиболее значимых прорывов в области численных методов за последние десятилетия.
Его уникальная способность существенно снижать вычислительную сложность и требования к памяти при сохранении высокой точности результатов сделала его незаменимым в самых разных научных и инженерных дисциплинах. От астрофизики до квантовой химии, от вычислительной электромагнетики до механики— применение БММ позволяет решать задачи, ранее выходившие за пределы возможного. Поскольку технологии продолжают развиваться, а количество данных в научных вычислениях стремительно увеличивается, важность такого эффективного и масштабируемого метода только возрастает. Быстрый мультипольный метод открывает новые горизонты в моделировании и оптимизации сложных систем, стимулируя дальнейшие исследования и внедрение инновационных вычислительных алгоритмов.