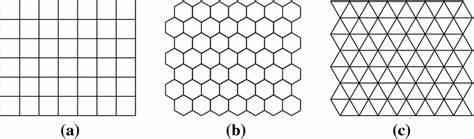
Традиционные сетки часто ассоциируются с квадратными ячейками, и это неудивительно, ведь квадратная сетка — наиболее привычная и простая для понимания структура. Однако, по мере развития технологий и усложнения задач, возникла необходимость в использовании более сложных и разнообразных структур сеток, среди которых особое место занимают треугольные и шестиугольные сетки. Они перестали быть просто альтернативой и стали полноценно конкурировать с квадратными сетками, проявляя уникальные свойства и предлагая новые возможности для решения широкого спектра задач. Преимущества нестандартных сеток объясняются их геометрическими особенностями. Треугольники, как простейшие многогранники, позволяют создавать адаптивные и гибкие модели.
Благодаря своей универсальной конфигурации, треугольные сетки легко поддаются юстировке и могут точно отображать кривые поверхности. Это крайне важно в компьютерной графике, когда моделирование сложных форм требует максимальной точности и эффективности. Шестиугольные сетки, в свою очередь, благодаря своей плотной упаковке и равномерному распределению узлов, обеспечивают оптимальное покрытие и минимизируют искажения, что особенно критично в геоинформационных системах и анализе растровых данных. Одна из уникальных особенностей шестиугольной сетки — ее способность эффективно поддерживать равномерную связанность между ячейками. В отличие от квадратной сетки, где каждая ячейка имеет четыре или восемь соседей в зависимости от рассматриваемой модели, шестиугольные сетки обеспечивают шесть равномерно распределенных соседей.
Это способствует более естественным моделям распространения информации или материалов, таких как поток воды, тепла или болезней. Кроме того, шестиугольные модели активно используются в симуляциях биологических и социальных систем, где взаимодействия имеют многогранный характер. Треугольные сетки заслуживают отдельного внимания благодаря своей универсальности. Они являются базисом для триангуляции Делоне — мощного математического инструмента, применяемого для оптимизации сеток и построения выпуклых оболочек. Это решение широко используется в обработке изображений, 3D моделировании, а также в инженерных расчетах, где важна точность и надежность сеточных структур.
Благодаря возможности легко адаптироваться к изменениям геометрии и варьировать размер ячеек, треугольные сетки становятся незаменимыми в сфере компьютерного моделирования и анализа сложных поверхностей. Современные инструменты и библиотеки для работы с сетками, такие как GridKit, активно развивают поддержку разнообразных форм сеток. Одним из ключевых преимуществ таких решений является возможность seamlessly переключаться между квадратными, треугольными и шестиугольными сетками, комбинировать их в рамках единой системы и адаптировать под конкретные задачи. Это обеспечивает гибкость и эффективность в обработке пространственных данных, визуализации, анализе растров и векторных данных, и открывает новые горизонты для научных и инженерных исследований. В контексте анализа природных процессов и моделирования ландшафта, шестиугольные сетки часто применяются для более точного отображения рельефа и распределения характеристик поверхности.
Благодаря равномерной форме ячеек и оптимальному соседству, они позволяют лучше отслеживать распространение фильтрации, осадков и других экологических параметров. Треугольные сетки, в свою очередь, подходят для адаптивного моделирования сложных геометрических структур, например, береговых линий, горных хребтов или городских ландшафтов. В области компьютерных игр и визуализаций использование нестандартных сеток открывает новые возможности для создания реалистичных карт и моделей. Шестиугольные сетки, из-за своей симметричной и органичной структуры, идеально подходят для построения игрового мира с равномерным распределением элементов и удобной навигацией. Треугольные сетки позволяют детально проработать поверхности и объекты, обеспечивая плавность и реалистичность визуализации.
Рассматривая перспективы развития технологий работы с сетками, становится очевидно, что концепция обязательной квадратной сетки уходит в прошлое. Современные платформы и библиотеки поддерживают мультиформатность сеток, что делает возможным гибкое применение каждого типа ячеек согласно требованиям конкретной задачи. Это повышает производительность алгоритмов, упрощает обработку больших данных и расширяет границы возможного в научных исследованиях и индустриальных приложениях. Таким образом, расширение представления о сетках и признание треугольников и шестиугольников как равноценных с квадратами представителей имеют серьезное значение для всех областей, связанных с пространственным моделированием и анализом. Эти формы сеток обеспечивают новый уровень точности, гибкости и эффективности, что важно для создания надёжных моделей, качественной визуализации и комплексного анализа данных.
В будущем можно ожидать дальнейшее развитие методов работы с разнообразными сетками и их интеграцию в автоматизированные системы, что позволит решать ещё более сложные и масштабные задачи.