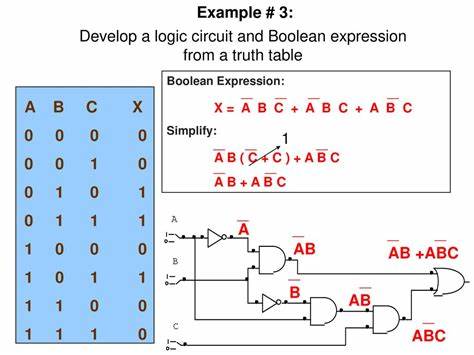
В 2020 году одна из значимых задач в теории булевых функций и логических схем была успешно решена: определение оптимальных схем для всех четырехвходовых двухвыходовых булевых функций. Этот прорыв открывает перспективы для разработки более эффективных цифровых систем и углубляет понимание их структурных особенностей. Булевы функции с четырьмя входами и двумя выходами представляют собой важный класс задач в области построения минимальных логических схем. Несмотря на то, что количество таких функций равно 2^32, что кажется огромным, благодаря симметриям и продуманному подходу к классификации возможно их систематическое исследование и оптимизация. Ранее исследования, проводимые Дональдом Кнутом в 2005 году, касались минимальной стоимости реализации пятивходовых булевых функций с одним выходом на базе двухвходовых логических вентилей.
Кнут определил, что существует всего шестнадцать 2-входовых вентилей с учетом затрат, при этом вентиль NOT — бесплатен с точки зрения стоимости. Сходный подход применён и к задачам с четырьмя входами и двумя выходами, но с заметным усложнением из-за увеличения количества выходных функций. Ключевой элемент исследования — учёт эквивалентных классов булевых функций по группе симметрий, включающей в себя перестановки и отрицания входов и выходов. Для задач с пятью входами и одним выходом размер группы симметрий составляет 7680, тогда как для задач с четырьмя входами и двумя выходами — 3072. Таким образом, количество уникальных классов эквивалентности подскочило до 1 476 218, что значительно усложняет задачу обработки и поиска оптимальных схем.
Для преодоления этой сложности была применена методика поиска в ширину (breadth-first search) с использованием оптимизаций и учётом групповых симметрий. Такой подход позволил эффективно просканировать пространство функций и реализовать для каждой из них минимальную стоимость схемы, базирующейся на двухвходовых и одно-входовых приёмах. Несмотря на экспоненциальный рост числа возможных комбинаций, удалось просчитать и сохранить в память структуру поиска до глубины 8, включающую миллиарды уникальных узлов. В процессе исследования особое внимание уделялось классификации по стоимости реализации. Были сформированы наборы представителей классов различной сложности: от самых простых, где стоимость равна нулю, до максимально сложных, достигающих стоимости 11 вентилей.
Пример самых простых функций — константные нулевые функции, либо выходы, повторяющие один из входных сигналов. Высокоустойчивые функции с максимальной стоимостью требуют сложных построений и были выделены в отдельный список для особого изучения. Для верификации результатов по верхней границе стоимости минимальной схемы был использован дополнительный фактический перебор всех функций и проверка наличия реализующих схем из базы данных. Это позволило удостовериться в корректности алгоритма и точности найденных верхних оценок. Более того, дальнейшие независимые поиски, проведённые с оптимизированным кодом, подтвердили совпадение полученных данных с предыдущими результатами, что повышает доверие к достигнутым выводам и обеспечивает большую надёжность.
Современные алгоритмы и инструменты синтеза булевых схем, описанные в этом исследовании, раскрывают новые возможности для разработки программируемых логических устройств и интегральных микросхем с оптимизированными параметрами. Наличие такой обширной базы оптимальных схем ускоряет процесс проектирования и позволяет создавать более компактные и энергоэффективные устройства. Также это открывает двери для дальнейших исследований в направлении увеличения числа входов и выходов, а также изучения многовыходных функций с большим числом параметров. Исследование 2020 года в значительной степени способствует развитию цифровой логики, становясь основой для будущих проектов в области аппаратного обеспечения, алгоритмической оптимизации и теории вычислительных систем. Особенность работы также в том, что подробные результаты и база данных открыты для сообщества, что способствует сотрудничеству и развитию новых методов в области оптимизации булевых функций.