Визуализация градиентного спуска: как понять и применить алгоритм шаг за шагом

Цифровое искусство NFT

Градиентный спуск — это один из фундаментальных алгоритмов в области машинного обучения и оптимизации, который помогает находить минимумы функций, оптимизируя модели и улучшая их точность. Понимание принципов работы градиентного спуска имеет решающее значение для тех, кто хочет глубже освоить машинное обучение, искусственный интеллект и анализ данных на практике. Визуализация градиентного спуска играет ключевую роль в облегчении усвоения сложных концепций, делая процесс обучения более наглядным и интуитивно понятным. Градиентный спуск используется для минимизации функции ошибки, которая измеряет, насколько хорошо модель предсказывает данные. Идея алгоритма состоит в том, что начиная с некоторой точки, мы постепенно движемся в направлении самого быстрого убывания функции, используя производную по параметрам модели.

При этом параметр шага движения, известный как скорость обучения, существенно влияет на эффективность и скорость сходимости алгоритма. Визуализация помогает увидеть, как именно меняются значения параметров модели по мере прохождения итераций, и что значит движение «вниз по склону» функции ошибки. Традиционные числовые и математические представления могут быть сложны для начинающих, но интерактивные приложения и мини-лабы делают процесс обучения понятным и увлекательным, наглядно демонстрируя ход работы алгоритма. Инструмент Gradient Descent Visualiser, разработанный командой Teach LA, представляет собой интерактивное приложение, предназначенное для ознакомления с алгоритмом градиентного спуска. Он стал отличным дополнением к курсам, посвящённым линейной регрессии и основам машинного обучения.

Визуальный инструмент позволяет пользователю задавать начальные условия, выбирать функции для оптимизации и настраивать параметры, такие как скорость обучения и стартовая точка. Такой подход способствует гораздо глубокому пониманию сути алгоритма за счет непосредственного участия. Работа с визуализатором начинается с выбора функции, которую необходимо минимизировать. Чаще всего это простая функция с одним параметром, например, квадратичная функция. Приложение отображает график функции, позволяя видеть её форму и выделять текущую точку, в которой находится алгоритм.

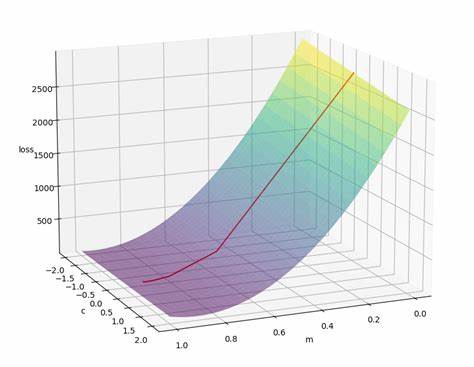
С каждым шагом градиентного спуска позиция точки изменяется, что можно наблюдать в режиме реального времени. Это позволяет понять, как параметр обновляется и движется к минимуму. Одним из важнейших аспектов является выбор скорости обучения — слишком большой шаг может привести к скачкам и даже уходу алгоритма от минимума, в то время как слишком маленький замедлит процесс. Визуализатор дает возможность отрегулировать этот параметр и наблюдать последствия в интерактивном режиме, что способствует формированию интуитивного представления об оптимальных значениях этого параметра. Применение градиентного спуска в линейной регрессии особенно демонстративно.

Задача сводится к нахождению коэффициентов элемента модели, минимизирующих среднеквадратичную ошибку между предсказаниями и реальными значениями. Визуализация помогает увидеть, как ошибки последовательно сокращаются, а параметры приближаются к оптимальным значениям. Это жизненно важно для понимания фундаментальных принципов регрессии и машинного обучения в целом. Кроме того, визуализация позволяет исследовать и сложности, возникающие при применении градиентного спуска к более сложным функциям. Например, функции с несколькими локальными минимумами или не выпуклые функции часто приводят к сложной динамике алгоритма.

Наблюдение за поведением градиентного спуска на таких функциях способствует осознанию ограничений классического алгоритма и необходимости использования более продвинутых методов, таких как стохастический градиентный спуск или методы с моментумом. Интерактивные мини-приложения, подобные Gradient Descent Visualiser, широко используются в образовательных целях. Они дополняют традиционные учебники и лекционные материалы, делая адаптивное обучение более эффективным. Для многих студентов и специалистов, которые только начинают знакомство с машинным обучением, такие инструменты становятся отличной отправной точкой для дальнейшего изучения глубоких нейронных сетей и более сложных моделей. В дополнение к интерактивному инструменту, Teach LA предлагает полезные ресурсы, которые дополнительно разъясняют теорию и практику градиентного спуска.

Учебные тетради и слайды помогают закрепить понимание, связывая визуальный опыт с формальными математическими выкладками. Среди рекомендованных материалов также есть курсы от ведущих мировых образовательных платформ и научные работы, дающие глубокий теоретический фон. Кроме обучения алгоритму, визуализация градиентного спуска полезна в реальных задачах анализа данных и разработки моделей. Понимание динамики обучения может помочь при отладке моделей, выборе гиперпараметров и поиске ошибок в данных. Благодаря интуитивному взгляду на процесс оптимизации специалисты и разработчики получают дополнительные инструменты для повышения качества своих моделей.

Стоит отметить, что современная область машинного обучения предлагает множество вариаций градиентного спуска, включая пакетный, стохастический и мини-пакетный подходы. Каждый из этих методов имеет свои достоинства и области применения. Визуализаторы помогают ориентироваться в этой множественности, показывая различия динамики и поведения алгоритма в зависимости от используемой стратегии. В эпоху стремительного развития искусственного интеллекта владение инструментами визуализации становится неотъемлемой частью арсенала каждого специалиста по данным. Это не только облегчает процесс обучения, но и ускоряет разработку эффективных и надежных моделей для решения разнообразных задач — от прогнозирования и кластеризации до создания интеллектуальных систем с элементами самосовершенствования.

Таким образом, визуализация градиентного спуска — это мощный и эффективный метод для глубокого понимания одного из ключевых алгоритмов машинного обучения. Использование интерактивных приложений способствует формированию прочных знаний и навыков, необходимых для успешной работы с современными интеллектуальными системами. Для всех, кто желает освоить машинное обучение, нельзя переоценить значение таких инструментов в образовательном процессе и практической деятельности.