Как односторонний автомат Правило 30 формирует двумерную вселенную игры Жизнь Конвея

Анализ крипторынка Юридические новости

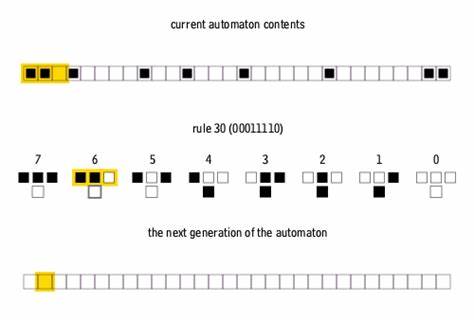
Клеточные автоматы представляют собой увлекательный класс дискретных моделей, которые эволюционируют во времени согласно простым, но мощным правилам. Среди множества таких автоматов Правило 30 занимает особое место благодаря своей непредсказуемой и хаотической динамике в одномерной среде. Объединение этого одномерного автомата с двухмерной средой известной игры Жизнь Конвея открывает новые горизонты для понимания сложных систем и генерации интересных паттернов. Правило 30 было предложено и популяризировано Стивеном Вольфрамом и является классическим примером одного из самых простых клеточных автоматов с удивительно сложным поведением. Оно работает на одной строке клеток, каждая из которых может принимать состояние 0 или 1.

В основе новой генерации строки лежит состояние текущей клетки и ее соседей, согласно фиксированному бинарному правилу, называемому Правило 30. Несмотря на простоту своей конструкции, автомат демонстрирует хаотические эффекты, порождая практически нерегулярные узоры, которые с трудом поддаются предсказанию или сжатию. С другой стороны, игра Жизнь Конвея - один из самых известных двухмерных клеточных автоматов, который эволюционирует на бесконечной сетке клеток, где каждая клетка может жить, умереть или возникать в зависимости от количества живых соседей. Эта модель наглядно демонстрирует сложное поведение из простых правил, включая стабильные образования, осцилляторы и самовоспроизводящиеся структуры. Идея подачи вывода Правила 30 в качестве начального состояния для игры Жизнь Конвея представляет собой уникальный мост между одномерной и двумерной динамиками.

Первоначальная строка, сформированная в соответствии с Правилом 30, становится своеобразной "опорой" или стартовой линией для двумерной вселенной Жизни. Таким образом, хаотичность и непредсказуемость одномерного автомата влияют на развитие сложных паттернов в двухмерном пространстве. Начальные условия начинают играть критическую роль в такой системе. Изменение стартовой строки, например, за счет добавления параметра "#seed=xxxx" в URL, позволяет генерировать разные вариации исходных данных. Каждый уникальный seed создает свой собственный вариант стартового состояния, способный привести к совершенно различным эволюциям во времени.

 

Это открывает широкие возможности для экспериментов и анализа влияния микросостояния начала на макро-паттерны. Совмещение этих двух систем, Правила 30 и Игры Жизнь, позволяет исследовать вопросы синергии между хаотическими и упорядоченными процессами. В этом контексте важно отметить, что выход одномерного автомата используется лишь как стартовая конфигурация, однако дальнейшая динамика управляется уже правилами двумерного пространства. Таким образом, формирование закономерностей и их последующая эволюция становятся объектом анализа для специалистов в области вычислительной физики, теории сложности и искусственного интеллекта. Функционально такая концепция реализуется путем преобразования одной строки в двумерную матрицу, где каждая ячейка стартового состояния соответствует области с активной или неактивной клеткой в игре Жизни.

 

После этого запускается классический механизм обновления клеток согласно трехаминной схеме Жизни - выживание, рождение, смерть. Результат - динамическое развитие сложных фигур, порой демонстрирующих долгоживущие структуры, фрактальные узоры или саморазрушающиеся цепочки. Использование данной технологии несет потенциал в креативных индустриях, моделировании биологических процессов, генерации искусственного интеллекта и визуализации сложных систем. Представленные данные позволяют создавать уникальные визуальные композиции на стыке порядка и хаоса, что особенно ценно для цифрового искусства и образовательных платформ. При практике работы с такими системами стоит учитывать высокие требования к вычислительным ресурсам при больших размерах сетки и сложных паттернах.

 

Оптимизация кодовой базы и внедрение механизма раннего завершения цикла могут существенно повысить производительность и удобство работы с моделями. Одной из наиболее интригующих особенностей реализации является возможность быстро изменять начальные условия через параметр seed, что облегчает генерацию множества вариаций и последующий анализ влияния изменений на глобальную динамику системы. Такой подход позволяет научным сотрудникам и любителям проводить детализированные исследования, экспериментируя с бесконечным множеством комбинаций. Подводя итоги, можно отметить, что интеграция одномерного клеточного автомата Правило 30 с классическим двумерным клеточным автоматом игрой Жизнь Конвея задает новый вектор развития в изучении и визуализации динамических систем. Это синтезирует хаос и порядок, простоту и сложность, одномерное и двумерное, создавая платформу для глубокого понимания процессов самоорганизации и эволюции в искусственных и естественных системах.

Подобные модели продолжают вдохновлять исследователей, программистов и художников на создание новых проектов, пересекающих границы дисциплин и расширяющих горизонты познания. Свобода выбора начальных условий, яркая визуальная динамика и возможность масштабирования делает этот подход мощным инструментом как в научных, так и в творческих приложениях. .