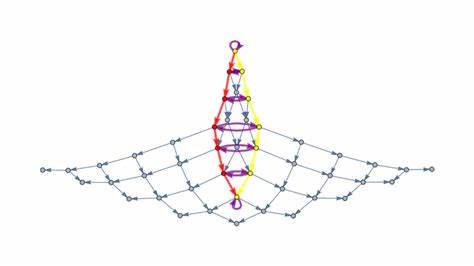
Современная математика и теоретическая информатика активно развивают сложные абстрактные модели для описания и анализа процессов, которые не подчиняются детерминированному поведению. Одной из таких моделей являются многопутевые (multiway) переписывающие системы — структуры, в которых множество возможных состояний и переходов развивается параллельно и недетерминировано. В статьях последних лет, в частности исследовании «Homotopies in Multiway (Non-Deterministic) Rewriting Systems as n-Fold Categories», проводятся глубокие рассуждения о том, как именно задавать и понимать гомотопии внутри этих систем с помощью категориального аппарата n-кратных категорий. Эти концепции становятся все более востребованными не только в категории теории, но и в математической физике и информатике, поскольку позволяют формализовать сложные структуры и преобразования с возможностью учета многократных связей и взаимодействий между объектами. Многопутевые переписывающие системы, как абстрактные машины, основаны на идее замены одних формальных выражений другими в соответствии с набором правил переписывания.
Однако, в отличие от детерминированных систем, где переход к следующему состоянию однозначно задан, в многопутевых системах имеются множественные варианты применения правил, каждое из которых порождает новое состояние. Эта особенность формирует граф состояний с ветвлениями в каждом узле и позволяет исследовать сложные динамические и гомотопические структуры. Важным понятием в изучении таких систем является гомотопия — способ понять, как разные пути или преобразования между объектами связаны друг с другом непрерывным образом, что становится особенно сложным в дискретных и недетерминированных контекстах. Для формализации гомотопий в многопутевых системах используется теория n-кратных категорий — обобщение обычных категорий, в которых объекты и морфизмы обобщаются до нескольких уровней. В таком аппарате можно рассматривать не только морфизмы между объектами, но и морфизмы между морфизмами, морфизмы между морфизмами морфизмов и так далее, что даёт возможность учитывать структуры гомотопий высших порядков.
Согласно результатам, показанным исследователями, включая Ксеркса Арсиваллу, Джонатана Горарда и других, многопутевая переписывающая система с гомотопиями до порядка n может быть сведена к структуре n-кратной категории. В этом случае морфизмы нижнего уровня представляют непосредственные установки правил переписывания, а морфизмы высших уровней — правила преобразования самих переписывающих правил, то есть гомотопии между ними. Такая конструкция становится особенной мощной при добавлении обратимых морфизмов, позволяющих формировать инвертируемые клетки и достигать структуры бесконечной категории, или ∞-группоида. Именно ∞-группоиды важны благодаря гипотезе гомотопии Гротендика, которая устанавливает глубокую связь между этими бесконечными когерентными категориями и гомотопическими пространствами. Таким образом, изучение многопутевых переписывающих систем в терминах n-кратных категорий не просто даёт новый язык для описания вычислительных процессов, но и позволяет перейти к топологическим и гомотопическим объектам, обладающим богатой структурой и имеющим применение в математической физике.
Эти приложения могут охватывать моделирование пространства-времени, квантовой гравитации, а также разработку новых формальных моделей вычислений с учетом многомерной информации и связи с топологией. Рассмотрение таких систем в контексте правил из так называемого «рульевого пространства» — множества всех возможных правил переписывания — даёт направление для изучения пространства всех возможных преобразований, что является важным для построения формальных математических моделей. Это пространство не является фиксированным, оно допускает включение и исключение правил, таким образом расширяя или сужая систему, и приглашая к размышлениям о вариативности и универсальности систем. Композиционные свойства этих структур актуальны для выявления связей между различными преобразованиями и для построения более сложных категорных моделей, где операции неразрывно связаны с операциями высшего порядка. В конечном итоге, изучение гомотопий и категориальных структур многопутевых переписывающих систем открывает перспективы для более глубокого осмысления вычислительных процессов и их топологических аспектов, связывая теорию вычислений, категорию теорию и математическую физику.
Такие исследования способствуют развитии нового понимания природы вычислений, их места в математическом моделировании и применении в физике, что в перспективе может повлиять на развитие фундаментальных теорий.