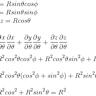Уравнения Навье-Стокса занимают центральное место в математической физике и теории гидродинамики, описывая движение вязкой несжимаемой жидкости. Эти уравнения были впервые введены в XIX веке и с тех пор вызывают огромный интерес как у математиков, так и у физиков. Их решение играет важнейшую роль в понимании сложных явлений турбулентности, потоков жидкости и газа и имеет ключевое значение для многих прикладных задач, включая аэродинамику, метеорологию и гидрологию. Несмотря на многолетние исследования, полное понимание свойств решений уравнений Навье-Стокса, особенно в трехмерном пространстве, остаётся одной из главных нерешённых проблем современной математики. Одной из наиболее значимых проблем является существование и гладкость решений в заданной области — именно этому посвящена новая работа Гэнцяня Лю, где был представлен прогресс в доказательстве существования гладких решений уравнений Навье-Стокса в трехмерном евклидовом пространстве.
Важность вопроса о гладких решениях уравнений Навье-Стокса трудно переоценить. Гладкое решение — это функция, обладающая всеми необходимыми степенями дифференцируемости, что позволяет применять к ней множество аналитических инструментов и обеспечивает физический смысл модели. Если гладкие решения существуют всегда и они единственны, это означает, что физическая модель течения жидкости предсказуема и надежна. Однако, если решения либо не существуют, либо нарушают гладкость, это приводит к непредсказуемости, появлению диагоналей и турбулентных режимов, что затрудняет моделирование и применение уравнений в реальных задачах. Традиционные методы исследования уравнений Навье-Стокса в трех измерениях вынуждены опираться на усреднённые данные или суженные классы решений, что не всегда отражает сложность реальных процессов.
Существующие доказательства в основном касаются двумерных случаев, где турбулентность и сложные динамические явления выражены гораздо слабее, либо относятся к слабым решениям, не гарантирующим гладкость. Новое исследование Лю основано на изучении так называемых параболических уравнений инерции Ламе — важного класса уравнений в теории упругости, который тесно связан с уравнениями Навье-Стокса через математическую структуру и кинематику движения жидкости. Ключевой идеей исследования стало доказательство существования и единственности гладких решений уравнений параболической инерции Ламе в трехмерной евклидовой среде. После этого появляется возможность перейти к уравнениям Навье-Стокса, рассматривая предел, при котором один из параметров Ламе, известный как константа λ, стремится к бесконечности, в то время как другой параметр μ остаётся фиксированным и положительным. В этом предельном переходе структура решений уравнений упругости преобразуется в такую, которая характеризует движение вязкой несжимаемой жидкости, то есть подходит под описание уравнения Навье-Стокса.
Таким образом, удалось построить непрерывный переход от одной математической модели к другой, сохраняя при этом свойства гладкости и единственности решений. Этот подход имеет несколько важных последствий. Во-первых, он открывает новый математический метод для исследования уравнений Навье-Стокса, который опирается на глубокое взаимосвязь с теориями упругости и параболическими уравнениями. Во-вторых, доказательство существования гладких решений в трехмерном пространстве — это шаг к решению одной из самых сложных задач математического анализа частных дифференциальных уравнений, которая входит в число знаменитых проблем тысячелетия. Успех в этой области способен значительно продвинуть понимание не только теоретических аспектов флюидодинамики, но и практического применения в инженерных и физических моделях.
Стоит отметить, что работа Гэнцяня Лю отличается особой внимательностью к деталям и глубиной доказательств. В третьей версии своей статьи, опубликованной в октябре 2025 года, автор добавил детальное разъяснение доказательства ключевой теоремы, что повышает прозрачность и доступность результатов для научного сообщества. Также в исследовании затрагиваются вопросы устойчивости решений и их поведение при изменении параметров, что важно для прикладных задач с разнообразными физическими условиями. Несмотря на позитивный настрой, научное сообщество тщательно проверяет новизну и обоснованность таких утверждений, учитывая историческую сложность проблемы. Исследование Лю является одним из самых актуальных и амбициозных результатов последних лет в области анализа дифференциальных уравнений, что уже привлекло внимание многих ведущих специалистов.
Дальнейшее развитие этого направления ожидается с использованием современных математических инструментов, таких как функциональный анализ, теория операторов и численные методы. Голос экспертов указывает на то, что открытие гладких решений для несжимаемых трехмерных уравнений Навье-Стокса может изменить подход к моделированию турбулентности, ликвидировав неопределённость и открыв дорогу к более точным прогнозам в метеорологии, аэродинамике и гидродинамике. Важность таких решений надежно связана с фундаментальной физикой, где каждая ступень гладкости влияет на интегралы движения и энергетические балансы системы. Из практической точки зрения, новые методы в решении уравнений Навье-Стокса позволят повысить эффективность симуляций, снизить вычислительные затраты и расширить возможности моделирования сложных инженерных систем. Турбулентные потоки, которые долгое время оставались главной загадкой гидродинамики, при помощи современных подходов могут получить более ясное математическое описание, что существенно расширит понимание динамики природных систем и технических процессов.
В заключение, можно сказать, что существование гладких решений уравнений Навье-Стокса в трехмерном евклидовом пространстве является одним из важнейших шагов в развитии современной математики и физики жидкости. Исследование Гэнцяня Лю представляет собой значительный прогресс в этой области и демонстрирует мощь применения междисциплинарных методов, объединяющих теорию упругости и гидродинамику. Продолжение работы в этом направлении обещает не только теоретические открытия, но и долгожданные приложения, способные изменить подход к анализу и расчету сложных динамических систем в реальном мире.