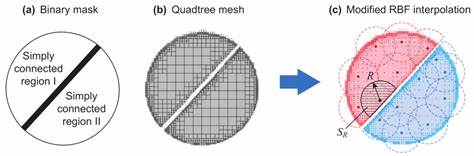
Создание качественных и визуально привлекательных градиентов является важной задачей в области компьютерной графики и веб-дизайна. Одним из популярных и эффективных методов для построения плавных mesh gradient, то есть градиентов с произвольной формой и насыщенностью цвета, является интерполяция с помощью радиальных базисных функций (Radial Basis Functions, RBF). Такой подход позволяет добиться уникального визуального эффекта, который сложно воспроизвести традиционными методами линейной или радиальной интерполяции цвета. Основная идея mesh gradient заключается в том, что цветовая область разбивается на сеть контрольных узлов, каждый из которых имеет свой цвет и положение. Градиент формируется за счет плавного перехода цветов между этими точками.
Однако сложность заключается в том, что необходимо обеспечить равномерную гладкость переходов по всей поверхности, особенно когда узлы располагаются неравномерно или имеют сильно различающиеся цвета. Интерполяция с использованием радиальных базисных функций позволяет корректно предсказывать значения цвета в любой точке плоскости, основываясь на расстоянии до ближайших контрольных узлов. В отличие от классических методов, RBF-метод применяет функцию, зависящую от радиального расстояния между точками, что обеспечивает более естественные и гладкие переходы. Популярные радиальные базисные функции включают многомерный гаусс, многомерный сплайн и многочлены Мультквада. Для реализации mesh gradient на базе RBF требуется определить набор контрольных точек с известным цветом.
После этого алгоритм строит интерполирующую функцию, которая минимизирует ошибку между заданными цветами узлов и вычисленными значениями по всей области градиента. Полученная модель позволяет в режиме реального времени вычислять цвет для любой координаты внутри градиентной сетки. Одним из главных преимуществ RBF интерполяции является её устойчивость к неравномерному распределению контрольных точек и способность легко обрабатывать сложные формы сетки. Это делает метод востребованным в дизайнерских инструментах, которые задают mesh gradient пользователям через интерактивный интерфейс. С точки зрения производительности, RBF-метод требует решения системы линейных уравнений, размер которой зависит от количества контрольных точек.
Для больших наборов данных используются оптимизации, такие как разбиение области на сегменты и применение разреженных матриц. В результате достигается баланс между качеством визуализации и скоростью рендеринга. При программировании mesh gradient на основе RBF важно учитывать форматы цветовых пространств и особенности визуализации на конечном устройстве. Рекомендуется работать с цветовыми моделями, которые позволяют легко интерполировать значения RGB или LAB, чтобы избежать нежелательных искажений цвета. Практическая реализация начинается с выбора подходящей библиотеки для работы с RBF, например SciPy для Python или специализированных модулей для C++ и JavaScript.
Затем осуществляется сбор контрольных точек и их параметров цвета, создается матрица расстояний и решается задача интерполяции. Наконец, рендеринг выполняется с вычислением цветов для каждой точки поверхности градиента. Mesh gradient на основе RBF интерполяции особенно полезен в веб-дизайне, визуализации данных и создании эффектов в графических редакторах. Он помогает повысить выразительность изображений, делая цветовые переходы более естественными и плавными, что положительно сказывается на восприятии конечного продукта пользователями. В заключение стоит отметить, что использование радиальных базисных функций для создания mesh gradient открывает широкие возможности для художественного творчества и технического совершенствования цифровой графики.
Этот метод заслуживает внимания специалистов, стремящихся создавать эффектные и качественные визуальные решения.