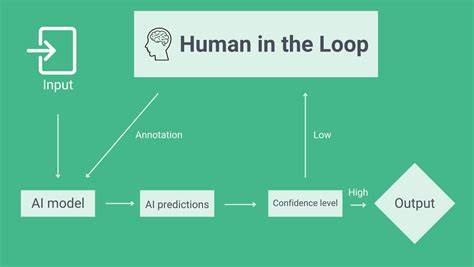
В современном мире искусственный интеллект (ИИ) занимает всё более значимое место в различных сферах жизни, от медицины и образования до искусства и промышленности. Совместная работа человека и ИИ, часто обозначаемая как взаимодействие в замкнутом цикле, становится основой для создания гибких, адаптивных и эффективных систем. Одним из основных вызовов при разработке таких систем является стабильность и надежность их работы, особенно при учёте технических ограничений, таких как квантование - процесс округления числовых значений при проведении вычислений. Последние исследования, основанные на мерах теоретического анализа, доказали, что взаимодействия человека и ИИ остаются устойчивыми даже при наличии ошибок квантования, что имеет фундаментальное значение для дальнейшего развития интеллектуальных систем.Понятие квантования касается дискретизации непрерывных величин в цифровых вычислениях.
Это неизбежный этап обработки данных в цифровых устройствах, где значения ограничены фиксированным числом бит. Вследствие этого происходит небольшое искажение числовых данных, что может негативно сказаться на работе алгоритмов. Для систем, основанных на сложном взаимодействии человека и ИИ, таких как системы совместного редактирования контента или голосовые помощники с взаимодействием на основе обратной связи, сохранение стабильности в условиях квантования особенно важно. Научная работа, проведённая учёными Фарука Алпая и Хамди Алаккада, предлагает строгий математический каркас для анализа таких систем и демонстрирует их стабильность, основываясь на свойствах измеримо-компактных множеств в пространстве L¹(μ).Основная идея разработки заключается в использовании теории неподвижных точек для отображений, которые являются нерасширяющимися (неexpansive maps) в функциональных пространствах.
В качестве математической модели взаимодействия между человеком, ИИ и квантователем выбрана композиция таких отображений, действующих на ограниченных замкнутых выпуклых подмножествах пространства L¹(μ). Благодаря свойству меры-compactness эти множества обладают фиксированной точкой, что соответствует устойчивому состоянию системы, где взаимодействие не приводит к бесконечным колебаниям или ошибкам, а достигается стабильный консенсусный артефакт.Интересно, что в своем подходе исследователи приняли во внимание реальные технические ограничения: квантование рассмотрено как малый возмущающий фактор на нерасширяющее отображение. Они доказали наличие приблизительных неподвижных точек, что говорит о том, что даже при учёте погрешностей округления стабильность системы сохраняется. Более того, были приведены контрпримеры, которые показывают, что используемые предположения являются оптимальными, то есть снижение требований к метрическим свойствам пространства или к компактности повлечёт потерю гарантированной стабильности.
Практическое значение этих результатов трудно переоценить. Многие современные системы, вовлекающие человека и ИИ в гибкое совместное принятие решений, сильно зависят от наличия устойчивого состояния, обеспечивающего согласованную и предсказуемую работу. К примеру, системы совместного редактирования документов или креативного контента с привлечением алгоритмов ИИ часто проходят через множество последовательных этапов, где действия человека корректируют предложения машины, а в ответ система подстраивается под изменения. Если взаимодействие такого рода подвержено нестабильности из-за технических ограничений, итоговый результат будет менее качественным или даже неадекватным. Благодаря теоретической гарантии устойчивости в условиях квантования, разрабатываемые системы смогут быть более надёжными и эффективными, что повысит доверие пользователей.
Также работа обладает значением для разработки алгоритмов в реальном времени и систем, где числовая точность ограничена вычислительными ресурсами, например в мобильных устройствах или embedded-системах с ограниченной производительностью. Возможность построения устойчивых циклов взаимодействия человека и ИИ при наличии квантования означает, что технологии могут стать более универсальными и адаптированными для широкого спектра приложений.С точки зрения методологии исследование объединяет несколько мощных направлений математики: функциональный анализ, теория динамических систем, измеримая компактность и теория неподвижных точек. Особое внимание уделяется свойствам нормальной структуры и равномерной интегрируемости, что позволяет аккуратно контролировать поведение отображений. Инновационное применение результатов Кирка, классической теоремы о неподвижных точках, к задачам взаимодействия человек-ИИ - пример успешной междисциплинарной синергии.
В контексте перспектив развития технологии и программного обеспечения для взаимодействия с ИИ отметим, что обеспечение стабильности взаимодействия не только улучшает качество работы систем, но и формирует основу для доверительных интерфейсов. Люди, взаимодействующие с интеллектуальными агентами, получают возможность более гладкого и предсказуемого пользовательского опыта, что позитивно влияет на адаптацию искусственного интеллекта в повседневной жизни. Таким образом, исследование подтверждает жизнеспособность концепции совместной работы человека и ИИ даже в условиях технических ограничений и ошибок, связанных с квантованием. Это открывает новые горизонты для создания устойчивых, адаптируемых и надёжных систем, способных эффективно функционировать в реальных условиях, что является важным шагом на пути к интеграции ИИ в повседневные процессы.В заключение стоит отметить, что результаты подчеркивают важность теоретического подхода к анализу практических систем и его роль в выявлении и обеспечении ключевых свойств, таких как устойчивость и стабильность.
Сложность современных задач взаимодействия требует глубокой математической базы для разработки новых технологий. Успехи в этой области расширят возможности ИИ и человека работать в тандеме, создавая инновационные и эффективные решения, учитывающие все особенности взаимодействия и технологические ограничения. Поэтому дальнейшее изучение мер компактности и неподвижных точек в контексте Human+AI является очень перспективным направлением для научных исследований и технологической реализации. .