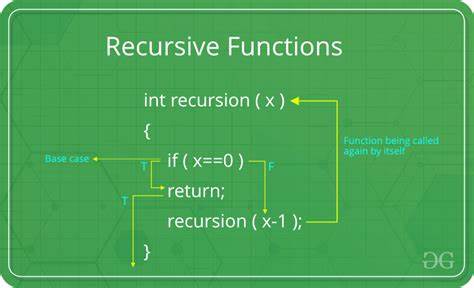
Рекурсия — один из самых фундаментальных и одновременно вызывающих споры подходов к решению задач в программировании. Принцип рекурсии заключается в том, что функция вызывает сама себя для решения подзадачи, которая приближает к окончательному решению. Несмотря на относительную простоту концепции, рекурсивные функции способны раздражать преподавателей компьютерных наук, особенно когда студенты придумывают хитрые версии, которые выполняют свою работу, но делают это очень неэффективно или выглядят чрезмерно усложненными. В этой статье мы рассмотрим несколько примеров рекурсивных функций, которые могут вывести из себя вашего профессора, но при этом будут технически правильными и рекурсивными. На основе этих примеров вы сможете лучше понять саму природу рекурсии, а также оценить баланс между теорией и практикой программирования.
Один из самых известных примеров — вычисление факториала числа. Факториал — это произведение всех натуральных чисел от 1 до заданного числа. Обычно рекурсивное вычисление факториала имеет простой базовый случай, например, факториал нуля равен единице, а основную часть реализации составляет умножение текущего числа на факториал предыдущего. Однако можно сделать процесс весьма своеобразным. Представьте функцию, которая для чисел от 0 до 20 содержит уже готовые результаты, хранящиеся в коде как отдельные условия.
Таким образом, для этих значений функция не производит вычисления и возвращает заранее известное значение. Такое решение технически является рекурсивным, ведь для чисел за пределами этого диапазона функция использует стандартный рекурсивный подход, но фактически рекурсия почти полностью отсутствует для массы случаев. Ирония в том, что подобный метод выглядит странно и неэффективно, но его можно считать корректным решением поставленной задачи. Следующий пример — вычисление чисел Фибоначчи. Последовательность Фибоначчи часто используется как классическое пояснение рекурсии, где каждый следующий элемент является суммой двух предыдущих.
Традиционно рекурсивная реализация проста, но в стандартном виде приводит к огромному количеству повторных вычислений для одних и тех же элементов. Чтобы решить этот вопрос, обычно применяется мемоизация — хранение ранее вычисленных значений. Тем не менее, можно написать функцию, в которой мемоизация реализована неэффективно: если запрашиваемое число отсутствует в кеше, функция итеративно вычисляет нужные значения и заполняет кеш, но затем все равно вызывает два рекурсивных вызова, которые, учитывая кеш, оказываются излишними. Эта реализация одновременно технически рекурсивна, но лишена практического смысла и демонстрирует уровень избыточности, вызывающий недоумение у тех, кто ожидает от рекурсии оптимального решения. Еще один забавный пример — использование рекурсии для проверки, является ли число четным или нечетным.
В программировании с этим обычно справляются за одну операцию с помощью остатка от деления на два. Рекурсивная же реализация выглядит как неоднократное уменьшение или увеличение числа в зависимости от его знака и постоянный вызов функции с обновленными значениями, где конечным базовым случаем становится проверка равенства нулю. Здесь паспособ рекурсии столь же забавен, как и неэффективен, особенно если дополнительно ввести параметр, указывающий, было ли число изначально положительным, раздробляющий логику и усложняющий понимание кода. Такая реализация, несмотря на свою техническую корректность, вызывает вопросы о необходимости применять рекурсию для задач, которые решаются гораздо проще и быстрее. Одним из серьезных и логически оправданных применений рекурсии является обход древовидных структур, например, в алгоритме глубинного поиска (DFS).
DFS применяют для поиска в графах или иерархических данных, где функция посещает ветви дерева рекурсивно, чтобы найти заданный элемент. Примером может служить структура, где каждый узел содержит пару ключ-значение и список дочерних узлов. Функция проверяет ключ текущего узла, а если значения не совпадают, идет по всем ветвям, используя рекурсивные вызовы. Ироничным моментом может стать добавление в код случайного повторения обхода веток, когда при возникновении исключения поиска появляется повторная попытка получить результат с помощью рекурсии. Такая реализация, хотя и усложнена и замедлена, по-прежнему возвращает корректный результат, но вызывает раздражение из-за избыточности и хаотичности.
Страсти вокруг рекурсии связаны не только с технической стороной, но и с образовательным аспектом. Многие преподаватели склонны воспринимать рекурсию как сложную концепцию для начинающих, а нестандартные, запутанные или чрезмерно громоздкие реализации только усиливают трудности восприятия. Между тем, рекурсия вполне доступна для понимания, если объяснять ее шаг за шагом, с наглядными примерами и графическими иллюстрациями. Часто рекурсия используется не там, где она нужна, или применяется неэффективно, что приводит к ошибочным взглядам на ее полезность. По мнению некоторых специалистов, лучше всего ее использовать в задачах, где рекурсивный подход органичен и естественен — например, при работе с деревьями, фракталами, сортировками, которые подразумевают разбивку задачи на подзадачи одного типа.
Например, реализация нахождения факториала или чисел Фибоначчи служит скорее учебным упражнением для понимания рекурсии, но в промышленном программировании зачастую заменяется итеративными или динамическими решениями, которые быстрее и менее затратны по памяти. Важно помнить, что любая рекурсивная функция должна иметь базовые случаи для остановки рекурсии и так называемые рекурсивные случаи, в которых функция постепенно приближает аргумент к базовому. Без базового случая рекурсия вызовет бесконечное выполнение и, как следствие, ошибку переполнения стека. Однако забавно, что легкое изменение структуры базовых случаев, например, распределение предопределенных значений для части диапазона аргументов, может превратить рекурсивную функцию в нечто сложно поддающееся логическому осмыслению, но при этом остающееся рабочим кодом. Подобные шутливые реализации далеко не являются образцовыми, однако они иллюстрируют, насколько гибкой и одновременно хрупкой может быть концепция рекурсии.
Их рассмотрение полезно для программистов всех уровней, поскольку демонстрирует не только плюсы, но и потенциальные подводные камни рекурсивного программирования. Для тех, кто хочет глубже разобраться с рекурсией, существуют специализированные ресурсы, книги и видео-курсы, способные не только объяснить теорию, но и показать практические аспекты на примерах. Очень интересной является книга «Рекурсивная книга о рекурсии», которая разбирает тему с большой долей юмора и простого объяснения, что помогает снять страх перед рекурсивными алгоритмами. Таким образом, рекурсия — это не только инструмент для решения задач, но и поле для экспериментов, шуток и неординарных решений. Регулярное изучение различных подходов к реализации рекурсивных функций, даже самых странных, помогает лучше понимать алгоритмы и развивать критическое мышление в программировании.
Если вы хотите удивить или слегка разозлить вашего преподавателя, попробуйте привести на практике подобные примеры и обсудить с ним преимущества и недостатки каждого из них. Главное, подходите к этому с юмором и пониманием сложности темы, тогда даже самые раздражающие шутки не испортят процесс обучения, а наоборот сделают его ярче и интереснее.