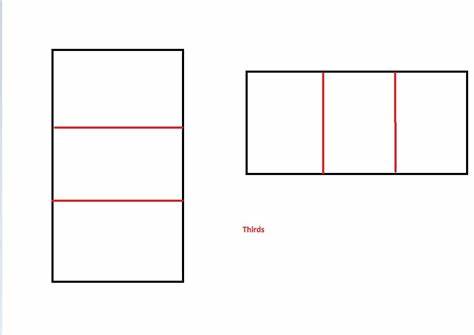
Разделение прямоугольника на равные части – задача, с которой сталкиваются многие в повседневной жизни, будь то приготовление еды, оформление интерьера, разметка для поделок или рукоделия. Казалось бы, для такой простой операции нужен только один инструмент – линейка. Но что делать, если её под рукой нет? Как разделить прямоугольник на три равные части без использования измерительных инструментов и при этом сохранить достаточную точность? Рассмотрим эффективные и проверенные методы, которые позволят справиться с задачей, опираясь на интуицию, базовые геометрические принципы и нестандартные подходы к измерениям. Начнем с простого: многие уверены, что разделить что-либо пополам без инструмента гораздо проще, чем на три части. И это действительно так.
Для половины достаточно найти середину, ориентируясь на визуальный баланс или пользуясь на глаз диагоналями. Для деления прямоугольника на две равные части можно наметить диагонали и, пересечением этих линий, определить центр. Затем провести линию, перпендикулярную одной из сторон через эту точку — так получают ровные половины. Однако задача разделить прямоугольник на три одинаковых частей значительно усложняется отсутствием простой центральной точки, которая бы указывала на точку деления. При этом появление инструментов, таких как линейка или рулетка, было бы естественным решением, но что если инструментов нет вовсе? Здесь становится полезным сочетание базовых элементов геометрии и практических наработок.
Один из подходов заключается в использовании диагоналей прямоугольника — линии, соединяющие противоположные углы. Проведя обе диагонали, мы получаем точку пересечения – центр прямоугольника. Этот центр служит отправной точкой для дальнейших построений. Следующий шаг — попытаться разделить угол или сторону с помощью определенных вспомогательных линий, которые помогут ориентироваться и получать линейные пропорции без дополнительных мер. Интересный метод предлагает построение линий цвета, обозначающих важные ориентиры.
Начинается с «красных» диагоналей, пересекающихся под углом 90 градусов. После этого стоит обратить внимание на линии, объединяющие центр и противоположные углы, условно обозначаемые «синим». Именно в точке пересечения этих линий закладывается точка, через которую можно провести линии деления прямоугольника на три части. Визуальная оценка и некоторый практический допуск играют важную роль при таком подходе. Хотя метод и стремится к максимальной точности, нанесение линий «по памяти», с помощью воображения и оценки на глаз, позволяет быстро получить удовлетворительный результат.
К примеру, можно мысленно определить среднюю точку верхней стороны, направить «красные» и «синие» линии через нее и далее продлить линию горизонтально или вертикально в зависимости от задачи разреза. Применение такого подхода особенно удобно, когда требуется разрезать что-то вроде противня с пирогом или слойки, где инструменты недоступны, а важна равномерность порций. На практике же после определения общей точки деления одна из частей – две трети – может быть дополнительно разделена на части с помощью глазомера, что не снижает общую аккуратность и эффективность разметки. Что немаловажно, данный алгоритм не ограничивается лишь плоской геометрией. Техника сохраняет свою работоспособность даже в условиях перспективного сокращения.
Это значит, что если смотреть на прямоугольник под углом или он изображен в перспективе, метод все равно поможет определить равные трети корректно. Такой подход ценен в дизайне, архитектуре и художественных работах, где точные пропорции важны, но использование стандартных измерительных средств ограничено. Для тех, кто стремится к максимальной точности и не хочет полагаться на визуальную оценку, можно дополнительно обратиться к простейшим законам алгебры и геометрии. При обозначении ширины прямоугольника буквой W, а высоты – H, можно описать уравнения линий, которые пересекаются в точках деления. Например, одна линия может быть описана как y = -H/W * x + H, другая – как y = 2H/W * x.
Поиск пересечения этих линий, даже решаемый при помощи доступных онлайн-калькуляторов, даст точные координаты точки, через которую нужно провести линию деления. Несмотря на некоторую сложность данного математического подхода, он служит базой для понимания геометрии задачи и помогает сформировать доверие к методике деления без измерительных инструментов. В конечном итоге, точность сильно зависит от требований пользователя: для кухни или хобби подойдет упрощенный, визуальный метод, для дизайна и архитектуры – более точный и подкрепленный расчетами. Подводя итог, можно утверждать, что разделить прямоугольник на три равные части без использования линейки вполне реально и достаточно удобно. Важным здесь является осознание геометрических принципов и практическая проработка линий, которые помогут ориентироваться на глаз.
Методы, основанные на построении диагоналей и определении точек пересечения, одновременно просты в понимании и эффективны в исполнении. Они позволяют не только быстро выполнить разметку, но и достичь приемлемой точности, особенно с практическим учетом времени и доступных ресурсов. Если вы столкнулись с необходимостью разделить прямоугольник в условиях, где нет измерительных приборов, не спешите отчаиваться. Обращайтесь к основам геометрии и не бойтесь экспериментировать с разметкой на глаз. Этот второй инструмент – ваше чувство пропорций и визуального баланса – окажется незаменимым помощником.
В завершение стоит отметить, что подобные методы и подходы не только помогают решать бытовые задачи, но и развивают пространственное мышление, а также понимание базовой геометрии, что всегда полезно в самых разных сферах жизни. Используйте эффектные лайфхаки, экспериментируйте, и вы убедитесь, что точные измерения доступны не только при помощи линейки, но и благодаря простому наблюдению и пониманию формы.