В статистике и машинном обучении при построении линейных моделей одним из важнейших этапов является выбор метода оптимизации параметров модели. Наиболее известными и широко используемыми подходами являются методы наименьших квадратов и наименьших абсолютных отклонений. Несмотря на то, что оба метода призваны минимизировать расхождение между предсказанными и наблюдаемыми значениями, у каждого из них есть свои особенности и области применения, которые существенно влияют на качество и надежность получаемой модели. Метод наименьших квадратов уже давно является золотым стандартом в задачах линейной регрессии. Суть его заключается в минимизации суммы квадратов разностей между фактическими наблюдаемыми данными и предсказанными значениями модели.
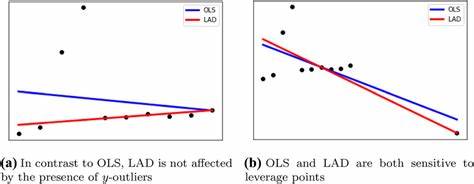
Такая постановка задачи обеспечивает простоту решения, поскольку приводит к системе линейных уравнений, которую можно эффективно решить аналитическими методами. Важной характеристикой этого метода является то, что он стремится минимизировать среднее квадратическое отклонение, что гарантирует, что итоговая модель будет в среднем максимально близка к реальным данным. Однако, несмотря на свое удобство и популярность, метод наименьших квадратов демонстрирует низкую устойчивость к выбросам — наблюдениям, которые значительно отличаются от общей тенденции данных. Причина этому кроется в квадратичной мере ошибки: каждый большой отклоняющийся объект получает вес, пропорциональный квадрату расстояния до модели, что может сильно искажать результат обучения. Например, если в выборке присутствует несколько экстремальных значений, то модель может чрезмерно «подгоняться» под них, теряя способность адекватно описывать основное распределение данных.
В этом контексте метод наименьших абсолютных отклонений (МНО) представляет собой альтернативный подход. Вместо суммирования квадратов отклонений он минимизирует сумму абсолютных значений разностей между наблюдаемыми и предсказанными значениями. Это приводит к тому, что каждая ошибка учитывается с одинаковым весом, вне зависимости от ее величины, что значительно повышает устойчивость модели к выбросам и аномалиям в данных. Результат такой оптимизации можно интерпретировать как минимизацию медианного отклонения, в отличие от метода наименьших квадратов, который фактически минимизирует среднее отклонение. Теоретически при включении в модель константного члена можно провести сравнительный анализ по условию стационарности производных целевой функции по параметрам.
Для метода наименьших квадратов сумма отклонений от модели равна нулю, что гарантирует, что модель в среднем совпадает с наблюдаемыми значениями. В случае метода наименьших абсолютных отклонений балансировка обеспечивается через равенство количества положительных и отрицательных отклонений, то есть медиана ошибок стремится к нулю. Следующее отличие методологии связано с функциональной формой вероятностной модели ошибок. Метод наименьших квадратов соответствует предположению, что ошибки распределены по нормальному закону с нулевым средним и постоянной дисперсией. В то время как метод наименьших абсолютных отклонений соответствует предположению о двойном экспоненциальном (распределении Лапласа) распределении ошибок.
Это отражается на способах обработки и весах ошибок, а также на характере оценки параметров модели. Практическое значение этих различий проявляется особенно ясно при работе с реальными данными, где высокая вероятность присутствия ошибок измерения, выбросов или просто редких экстремальных наблюдений. При таких обстоятельствах стандартный метод наименьших квадратов может привести к переобучению модели под редкие и сильные аномалии, существенно снижая качество предсказаний на новых данных. Метод наименьших абсолютных отклонений, благодаря своей повышенной устойчивости, позволяет построить более стабильную и надежную модель, которая лучше отражает основные тенденции данных. Тем не менее, стоит отметить, что метод наименьших абсолютных отклонений сложнее в реализации, в частности, из-за отсутствия простого аналитического решения, как в случае квадратов ошибок.
Обычно для него применяются численные методы оптимизации, что приводит к увеличению вычислительной нагрузки. В связи с этим при работе с большими объемами данных и при отсутствии значительных выбросов традиционный метод наименьших квадратов остается предпочтительным выбором. Еще одним интересным аспектом выбора между двумя подходами является их чувствительность к распространению данных. Метод наименьших квадратов, будучи чувствительным к большим отклонениям, активно учитывать широкий спектр вариаций и может быть успешен в ситуациях, где данные подчинены нормальному распределению с малым количеством выбросов. Метод наименьших абсолютных отклонений эффективен в случаях, когда ожидается, что большая часть данных сосредоточена вокруг медианы, а выбросы могут иметь существенно искажающее влияние.
Кроме того, современные методы машинного обучения комбинируют преимущества обоих подходов, адаптируя функции потерь и применяя различные техники регуляризации, что позволяет автоматически обнаруживать и смягчать влияние экстремальных значений. В частности, модели с гибкой функцией потерь, например, Huber loss, совмещают квадратичную ошибку для малых отклонений и абсолютную ошибку для больших, что часто дает наилучшее соотношение между качеством и устойчивостью модели. С точки зрения анализа и интерпретации, понимание того, что метод наименьших квадратов оптимизирует среднее отклонение, а метод наименьших абсолютных отклонений – медиану, помогает лучше выбирать стратегию под конкретные задачи. Если целью является предсказание с низкой чувствительностью к выбросам и значениями, которые могут быть аномально высокими или низкими, предпочтение стоит отдавать медианному подходу. В случаях же, когда важна подгонка под общую тенденцию без нарушения средней ошибки, выбор падает на классический метод наименьших квадратов.
С точки зрения теоретической базы, мало кто подвергает сомнению право метода наименьших квадратов, учитывая его тесную связь с классической статистикой и многочисленными теоремами, такими как Гаусса-Маркова. Однако в прикладных задачах и анализе больших данных, где требования к устойчивости предсказаний возрастают, наибольший интерес представляют альтернативные методы оценки, включая рассмотренный метод наименьших абсолютных отклонений. В итоге при проектировании регрессионной модели необходимо оценивать характер данных, наличие выбросов, требований к точности и устойчивости, а также вычислительных ресурсов. Именно в балансе всех этих факторов и заключается оптимальный выбор между минимизацией суммы квадратов и суммы абсолютных отклонений. При наличии возможности экспериментальной проверки моделей лучше всего реализовать оба метода, сравнить их результаты на валидационных данных и сделать осознанный выбор, ориентируясь на конечные цели задачи.
Подытоживая, методы наименьших квадратов и наименьших абсолютных отклонений представляют два фундаментальных пути решения одной и той же проблемы – минимизации разницы между измерениями и моделью. Первый оптимизирует среднее значение ошибки, что подходит при нормальном распределении ошибок и отсутствии резких выбросов. Второй – ориентирован на медиану, что значительно повышает устойчивость к экстремальным значениям и шуму в данных. Понимание механизма работы и последствий выбора каждого из этих методов чрезвычайно важно для качественного построения и интерпретации регрессионных моделей в самых разнообразных прикладных областях.