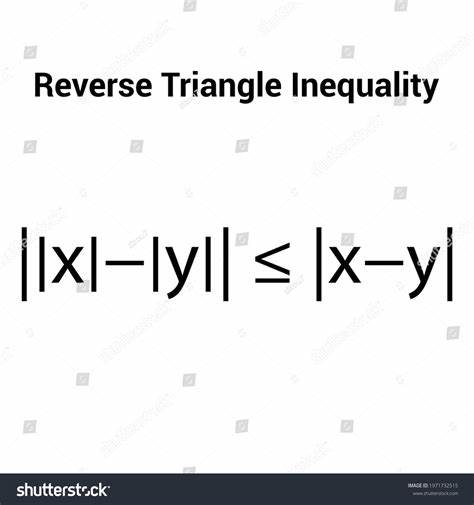Неравенство треугольника — фундаментальный принцип, хорошо известный каждому, кто сталкивался с геометрией и метриками. Его суть проста и ярко иллюстрирует важный геометрический факт — самый короткий путь между двумя точками лежит по прямой. Записывается это как |AC| ≤ |AB| + |BC|, что означает, что расстояние от точки А до точки С не превышает суммы расстояний от А до В и от В до С. Однако существует и загадочная концепция, называемая обратным неравенством треугольника, которая вносит свою уникальную ноту в понимание процессов не только в математике, но и в программировании и организации работы. Именно ей и посвящено наше подробное рассмотрение.
Обратное неравенство треугольника выражается символически так: |AC| > |AB| + |BC|. На первый взгляд кажется, что это противоречит здравому смыслу и классическим теориям. Но в программной инженерии и менеджменте проектов оно обретает своеобразный метафорический смысл. В контексте программирования нередко оказывается, что добраться от состояния А к С напрямую сложнее и ресурсоемче, чем через промежуточную точку В — например, благодаря делению задачи на более мелкие подзадачи, промежуточным проверкам и корректировкам. Изучение этой концепции важно не только для тех, кто занимается математикой — она может вдохновить разработчиков, менеджеров проектов и исследователей на поиск новых подходов к решению сложных задач.
Чаще всего в жизни и работе сталкиваемся с ситуациями, когда попытка сразу добраться до конечной цели оказывается «дорогой» с точки зрения затрат времени и усилий. Промежуточная остановка или этапы с меньшими задачами позволяют значительно снизить сложность и улучшить качество результата. Рассматривая классическое неравенство треугольника, легко заметить, что оно работает не только в классической евклидовой геометрии, но и многомерных пространствах с различными способами измерения расстояния. Например, в так называемой метрике Манхэттена расстояние между двумя точками определяется как сумма абсолютных разностей координат по горизонтали и вертикали. Несмотря на различия, неравенство треугольника там тоже сохраняется.
То же касается и таких сфер, как вычисление расстояния Левенштейна между строками ДНК, что имеет огромное значение в биоинформатике. Эта универсальность делает неравенство мощным инструментом, формирующим представления о метриках и пространствах, на которых строятся многие алгоритмы и модели. В программировании одном из ключевых практических применений метафоры обратного неравенства треугольника является управление изменениями и исправлениями в коде. Существует стойкое и до недавнего времени мало формализованное правило: большие изменения сложны для восприятия, проверки и интеграции, тогда как небольшие, независимые изменения вносятся быстрее, а контроль качества становится проще. Эта идея тесно связана с кубиками работы и pull request (PR) — механизмом внесения правок в проекты с использованием систем контроля версий.
Лучше разбивать большие задачи на маленькие, понятные части, которые можно быстро проверить и протестировать. Такой подход сокращает время обратной связи, снижая риск возникновения конфликтов и неудач при интеграции. Крупные изменения, разбитые на мелкие шаги, становятся управляемыми и прозрачными. Иногда стоит понимать, что размер изменений—лишь внешний параметр. Действительный критерий — независимость работы и её логическая завершенность.
Даже если PR маленький по объему, но содержит сложное изменение логики, он требует тщательного рассмотрения, а наоборот — большой PR, представляющий множество простых и понятных изменений, может быть освоен быстрее. Важным элементом в редактировании кода является рефакторинг. Часто обновление системы подразумевает несколько последовательных шагов. Например, сначала стоит просто протянуть новый параметр через большинство функций, не меняя логику работы. Затем уже можно изменить логику с новым параметром.
Такой подход позволяет избежать одновременной работы с большим числом изменений и снижает сложность кода, который необходимо воспринимать и тестировать сразу. Методология тестирования и разбиения больших задач на мелкие подразделы имеет прямое отношение к качеству выпускаемых продуктов и к процессу релизов. Частые и небольшие выпуски, подготовленные маленькими шагами, позволяют быстрее получить обратную связь от пользователей, уменьшить риски ошибок и облегчить процесс исправления. Такой цикл релизов способствует более плавным улучшениям, чем редкие, массивные обновления с большим количеством потенциальных ошибок. С другой стороны, существует определённый компромисс в виде стратегии «глубоких изменений».
Это когда вместо множества маленьких шагов делается полное решение сразу, даже ценой сложной истории изменений и большей вовлеченности команды. Такой подход оправдан в случаях, когда важно не только быстро исправить проблему, но и фундаментально улучшить архитектуру, заложить прочную основу для дальнейшего развития. Обратное неравенство треугольника мотивирует программистов и менеджеров к поиску оптимального баланса между этими двумя подходами — быстрыми небольшими шага, каждый из которых закладывает стабильную платформу, и глубокой проработкой архитектуры и логики, которая может занять больше времени, но обеспечивает более качественный и надёжный результат. В реальных условиях специалисты часто комбинируют оба подхода. Первичная реализация может быть сделана быстро и аккуратно для проверки концепции, с последующей переработкой в более структурированную и удобную форму.
Такой метод снижает риски ошибочных решений и позволяет не терять перспективу глобальных целей при работе с частными задачами. Важно понимать, что программирование и разработка — по сути, сродни математическому моделированию сложных процессов. Идеи из теории метрик, такие как неравенство треугольника и его обратная версия, переходят в практические рекомендации, позволяя улучшить качество разработки, её скорость и предсказуемость. Подводя итог, обратное неравенство треугольника — не просто математический курьёз. Это приглашение задуматься о том, как мы организуем процесс работы, как расставляем приоритеты и как справляемся с комплексностью.
Концепция служит полезным напоминанием о том, что зачастую нужно делать шаг назад, прежде чем прыгнуть вперед, и что достижение цели через промежуточные моменты порой оказывается более эффективным. Осознание и внедрение этих принципов в повседневной работе — залог стабильного, качественного и управляемого развития как программных продуктов, так и личной профессиональной практики. Интеграция идей обратного неравенства треугольника в методологии разработки предоставляет новые пути оптимизации и совершенствования, подтверждая, что даже классические математические истины находят своей отражение в наших технических дисциплинах и жизни.