Хеш-функции играют ключевую роль в компьютерных науках, обеспечивая эффективное хранение и поиск данных, а также безопасность информации. В основе их работы лежит преобразование сложных, часто объемных данных — будь то текст, изображение или даже биометрические характеристики — в компактное числовое представление фиксированной длины. Это преобразование позволяет быстро идентифицировать и сравнивать объекты без необходимости обрабатывать весь исходный контент. Однако с развитием и масштабированием систем перед исследователями и разработчиками встает важная задача — понимание и минимизация вероятности коллизий хешей. Коллизия происходит, когда два разных объекта приводят к одинаковому хеш-значению, что способно вызвать ошибки в системах поиска и хранить нежелательные несоответствия.
Чтобы понять вероятность таких событий, необходимо обратиться к фундаментальной математической проблеме, известной как парадокс дней рождения, которая объясняет почему даже при большом количестве возможных значений коллизии случаются с неожиданно высокой вероятностью. Эта правда может показаться парадоксальной на первый взгляд: интуитивно кажется, что вероятность столкнуть два объекта в одну и ту же ячейку должна быть невысокой, особенно если количество «ящиков», в которые эти объекты помещаются, очень велико. Но природа вероятности и сочетаний работает иначе, чем наше обыденное восприятие. Рассмотрим классический пример: в комнате из 23 человек вероятность того, что хотя бы двое поделят день рождения, превышает 50%. Этот феномен возникает из-за того, что вероятность рассматривается не по каждому человеку отдельно, а по парам, количество которых растет квадратично с числом участников.
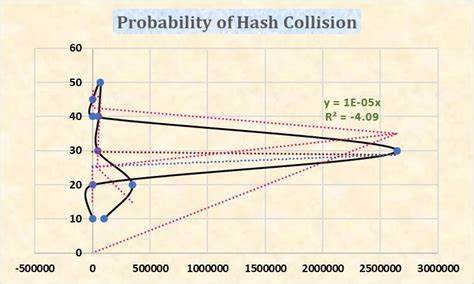
В мире хеш-функций ситуация аналогична. Если представить, что «ящики» — это возможные тысячи или миллионы значений хешей, а «шарики» — объекты или данные, которые мы хешируем, то при росте количества объектов вероятность того, что два из них попадут в один и тот же ящик, не просто растет, а растет с числом пар объектов. Для точного вычисления этой вероятности можно использовать формулу, вытекающую из подхода задачи о днях рождения: вероятность отсутствия коллизий равна произведению вероятностей того, что каждый последующий объект попадает в уникальный ящик. Соответственно, вероятность хотя бы одной коллизии — это единица минус это значение. Тем не менее при больших масштабах данных вычисление точного значения становится неэффективным из-за огромного количества вычислительных операций.
Здесь на помощь приходят приближённые методы. Один из популярных вариантов включает использование экспоненциальных приближений, которые сводят сложные произведения к простым формулам через экспоненту. Это позволяет оценить вероятность коллизии в зависимости от числа объектов и размера пространства хешей с большой точностью и значительно меньшими затратами вычислительных ресурсов. Еще более простые приближения используют формулу, пропорциональную квадратичному количеству пар объектов и обратно пропорциональную размеру пространства хеширования. Хотя эти формулы не столь точны, они часто достаточны для быстрого анализа и принятия решений в проектировании систем.
Проблема коллизий не ограничивается лишь теоретическими вычислениями. На практике они влияют на производительность баз данных, распределенных систем, криптографии и других областей. Хорошие хеш-функции должны равномерно распределять объекты, минимизируя коллизии. При проектировании систем важно учитывать ожидаемый размер данных и выбирать или настраивать хеш-функции и размер их пространства значений таким образом, чтобы вероятность коллизии оставалась минимально возможной. Иногда это означает использование более длинных хешей, увеличение числа «ящиков» или введение дополнительных уровней проверки и разрешения коллизий.
Понимание того, что коллизии неизбежны при достаточном объеме данных, помогает организациям планировать архитектуру своих систем с учетом необходимости обработки таких случаев, снижая риски потери информации или ухудшения производительности. Одним из примеров практического применения является база данных клиентов, где хеширование используется для анонимизации или быстрого доступа к информации. В таком случае коллизии могут привести к путанице, например, с заказами разных клиентов, что недопустимо. Следовательно, необходимо обеспечить огромный размер хеш-пространства и применять стратегии обнаружения и обработки коллизий. Современные вычислительные мощности и продвинутые математические подходы позволяют эффективно управлять этой проблемой, однако ключевым остается баланс между скоростью обработки, объемом памяти и допустимым уровнем ошибок.