В современном мире мы сталкиваемся с масштабными вызовами, связанными с управлением и координацией огромного числа людей. По оценкам, население планеты уже превысило отметку в 7 миллиардов человек, и вся эта масса людей требует стабильных систем управления, коммуникации и сотрудничества. Однако, несмотря на впечатляющие достижения в технологии и науке, задача эффективного управления и синхронной координации столь огромных групп людей остается чрезвычайно сложной. В последние годы ведущие исследователи из области вычислительной теории выявили глубокие параллели между управлением массовыми коллективами и сложными технологическими задачами, доказав, что даже базовые модели координации масштабируемы до неразрешимых или чрезвычайно сложных задач. Исследование, проведенное учеными Альессандро Панконе́зи, Пьетро Мария Поста и Мирко Джаккини, показывает, что теоретические основы управления тысячами, миллионами или даже миллиардами работников, представленных в форме программы, могут обладать вычислительной сложностью, сравнимой с известными классами NP-Hard или PSPACE-Hard.
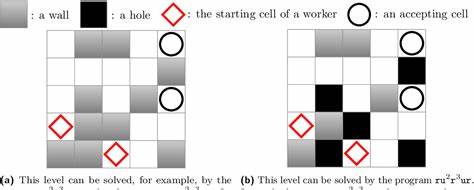
Это означает, что с точки зрения вычислительной сложности сама задача координации является крайне ресурсоемкой и, в целом, непростой для оптимального решения. Их работа, вдохновленная видеоигрой под названием "7 Billion Humans", иллюстрирует, насколько целенаправленное управление многими агентами, выполняющими одни и те же инструкции, может стать практически неразрешимым, даже если правила взаимодействия кажутся простыми. Видеоигра позволяет игрокам писать программы, которые запускаются одновременно на большом количестве виртуальных рабочих, направляя их к различным целям. Несмотря на интуитивно понятный геймплей, исследователи доказали, что даже упрощенные версии стратегии управления действительно соответствуют сложным классам вычислительной теории. Это открытие имеет глубокие последствия для реального мира, где управлять и координировать огромные группы людей гораздо сложнее, чем может показаться на первый взгляд.
В реальности человечество сталкивается с большим числом факторов, затрудняющих коллективную организацию: разнородность мотивации, ограниченное количество информации, ограниченная пропускная способность коммуникации, человеческие ошибки и непредсказуемость поведения. При этом теоретическая модель, основывающаяся на повторяющихся однородных агентах и строгих правилах, представляет собой даже более структурированный сценарий, чем реальность. Если в таком упрощенном случае координация уже демонстрирует высокую вычислительную сложность, то задача управления реальными социумами становится еще более масштабным вызовом. Одной из ключевых проблем является параллельное выполнение одних и тех же инструкций миллиардами агентов, где синхронизация, совместное преодоление конфликтов и достижение общей цели требуют огромных ресурсов. При этом даже малейшие изменения в правилах или целях могут привести к резкому увеличению сложности.
С точки зрения науки о вычислениях, NP-Hard и PSPACE-Hard - это классы задач, которые либо трудно решать за полиномиальное время, либо требуют значительных ресурсов памяти и вычислительной мощности. Аналогично, при координации больших человеческих масс сложность принятия решений и выделения оптимальных стратегий возрастает экспоненциально. Следствием этих ограничений являются многие социальные и экономические проблемы современности: сложности с глобальной организацией работы, распределением ресурсов, регулированием социальных процессов и обеспечением устойчивого развития. В эпоху глобализации, массовой миграции, цифровой трансформации и постоянных технологических изменений необходимость эффективных механизмов управления коллективами становится критически важной. Современные технологии, такие как искусственный интеллект, алгоритмы машинного обучения и распределенные вычисления, предлагают средства частичной автоматизации координации.
Однако и они сталкиваются с фундаментальными ограничениями, которые накладывает природа задачи и сложность моделей. Например, в больших организациях и социальных системах почти всегда присутствует децентрализация принятия решений, ограниченный обмен информацией между различными звеньями, а также неполная и запаздывающая обратная связь. Все это ухудшает возможность принятия оптимальных решений быстро и точно. В таких условиях стратегии построения устойчивых систем координации чаще всего сводятся к эвристическим методам, приближенным алгоритмам и гибкому управлению, адаптирующемуся к изменениям. Большое значение приобретает разработка систем с высокой степенью саморегуляции, когда отдельные участники или группы самостоятельно регулируют свои действия, подстраиваясь под изменяющиеся условия и окружение.
Кроме того, социальные и культурные факторы, такие как уровень доверия, нормы взаимодействия и наличие мотивации, играют важнейшую роль в формировании эффективных механизмов коллективного взаимодействия. Исследования из области вычислительной сложности, подобные описанным в работе Панконе́зи и коллег, позволяют лучше понять фундаментальные ограничения и потенциальные риски при масштабировании процессов координации на глобальном уровне. Они служат мощной математической основой для анализа систем коллективного поведения и разработки новых стратегий управления массами, которые будут реалистичными и эффективными. В итоге, вызов координации "7 миллиардов людей" - это не просто задача социальной инженерии, а глубокая междисциплинарная проблема, требующая объединения знаний в области компьютерных наук, математики, экономики, психологии и социологии. Только понимание технологических и теоретических барьеров позволит создать новые модели, поддерживающие человеческую деятельность в масштабах всей планеты.
Ключевым аспектом развития станет интеграция научных достижений с инновационными технологиями, направленными на гармоничное и эффективное взаимодействие различных сообществ и систем. Адресуя эти вызовы, человечество совместно сможет максимально эффективно использовать свой коллективный потенциал и создавать устойчивое будущее, где сложные задачи координации будут решаться с минимальными издержками и максимальной пользой для всех. .