Современные модели на основе архитектуры трансформеров кардинально изменили подход к обработке естественного языка и изображений. Одной из важнейших составляющих этих моделей является механизм позиционного кодирования, позволяющий учитывать порядок и относительное расположение элементов во входных данных. Среди различных методов позиционного кодирования особое внимание привлекают ротационные позиционные эмбеддинги (Rotary Positional Embeddings — RoPE), особенно их обобщение на случай N-мерного пространства. В данной статье мы подробно рассмотрим концепцию N-мерных ротационных позиционных эмбеддингов, их устройство, преимущества, а также практические аспекты использования и оптимизации в нейросетевых архитектурах. Роль позиционных эмбеддингов в трансформерах напрямую связана с необходимостью учитывать последовательность токенов или элементы данных, так как базовая архитектура трансформера по умолчанию не предполагает встроенного понимания порядка.
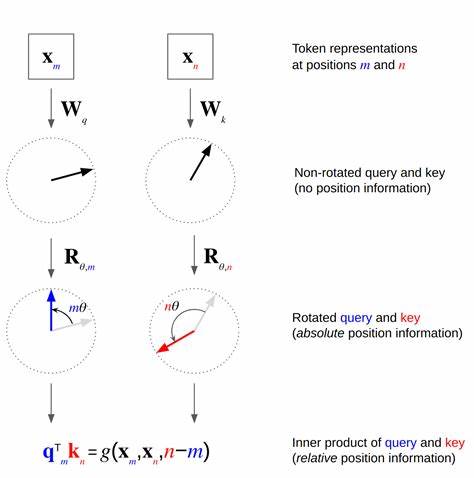
Традиционные подходы включают встраивание фиксированных или обучаемых векторов, которые добавляются к эмбеддингам токенов, но эти методы имеют ограничения с точки зрения представления относительных расстояний и общего влияния на механизм внимания. Ротационные позиционные эмбеддинги, впервые предложенные Су и соавторами в 2021 году, представляют собой оригинальный и эффективный способ кодирования позиционной информации. В данной методике к векторам запросов и ключей на каждом токене применяется преобразование вращения вектора в двумерных подпространствах, где угол вращения пропорционален позиции токена. Такой подход сохраняет пространственные и относительные отношения между элементами, при этом он позволяет добиться более точного и избирательного внимания к конкретным парам (ключ, относительная позиция). Традиционно RoPE применялся для одномерной позиции, например для текстовых последовательностей.
В этом случае дименсионность вектора делится на пары, и каждая пара подвержена вращению на угол, пропорциональный произведению частоты и позиции токена. Градиентные методы и структурные свойства оборачивания гарантируют, что комбинация нескольких частот сглаживает влияние, концентрируя внимание на определённых координатах. Однако современным задачам обработки изображений и видео необходим более сложный подход, так как данные имеют двумерную или даже многомерную структуру. Расширение RoPE на двумерное пространство реализовано в виде так называемого аксиального RoPE (axial RoPE), при котором половина измерений вращается с фактором, соответствующим горизонтальной координате, а другая половина — вертикальной. Несмотря на то, что аксиальный RoPE сохраняет относительную позиционную информацию и эффективен, он накладывает ограничения на точность локализации внимания.
Так, запросы не могут избирательно воздействовать на конкретные пары (ключ, позиция), а воздействие распространяется по строкам или столбцам. Решением этой проблемы стала инновационная идея измерять позиции токенов не только вдоль стандартных осей, но и по произвольным направлениям в пространстве. Это позволяет ротационным эмбеддингам осуществлять более тонкие и независимые вращения в каждой паре измерений, используя углы, пропорциональные проекциям позиции токена на выбранные направления. Данная концепция была отражена в работе Хео и коллег в 2024 году в рамках метода Mixed RoPE. Однако, не во всех случаях реализации он применяется корректно, зачастую ограничиваясь аксиальными методами.
В общем виде N-мерные ротационные позиционные эмбеддинги представляют собой композицию вращений в ортогональных двумерных подпространствах с углами, вычисленными через внутреннее произведение вектора позиции и набора единичных направлений, умноженных на частоты. Выбор направлений особенно важен для качества представления. Перемешивание направлений с использованием равномерного распределения по окружности, а также принципов золотого сечения позволяет получить более равномерное и эффективное покрытие пространства, что способствует повышению точности концентрации внимания на уникальных позиционных парах. Одной из ключевых практических новинок является Golden Gate RoPE — метод, при котором направления определяются через перестановки, основанные на золотом сечении и числовых последовательностях общего рода для больших размерностей. Это обеспечивает детерминированную и хорошо рассредоточенную инициализацию, что снижает необходимость дополнительного обучения частотных параметров и обеспечивает стабильную работу модели при изменении разрешения или длины последовательности.
На практике в задачах компьютерного зрения, таких как классификация изображений с помощью Vision Transformers (ViT), применение N-мерных RoPE показало значительное улучшение показателей качества по сравнению с традиционными методами позиционного кодирования. Так, на датасете CIFAR10 и ImageNet-1K модели с Golden Gate RoPE достигали более низких значений функции потерь (negative log-likelihood) и более высокой точности классификации. Особенно заметны преимущества при переходе к более высокому разрешению изображений на этапе инференса, где мягкое масштабирование позиционных кодов совместно с RoPE обеспечивает лучшую обобщающую способность. Эксперименты также подчеркнули важность подбора минимальных и максимальных частот вращения. В задачах языкового моделирования и обработки длинных последовательностей диапазон частот часто значительно шире и требует настройки с учётом масштаба координат.
Как правило, минимальная частота устанавливается примерно в интервале от 0.2 до 1.0, а максимальная — от 20 до 100 для изображений, при позициях нормированных в диапазон [-1.0, 1.0].
Оптимальный выбор влияет на способность модели выделять локальные и глобальные структурные паттерны. Обсуждение преимуществ N-мерных RoPE не ограничивается лишь качеством классификации. Они обеспечивают несколько важных свойств для механизмов внимания. Во-первых, за счёт мультичастотных вращений реализуется высокая избирательность относительно положения, что помогает избегать размывания внимания. Во-вторых, возможность оперировать с произвольными направлениями в позиционном пространстве расширяет спектр структурных свойств, доступных модели, включая инвариантность и устойчивость к изменениям параметров входных данных.
Однако данная методика также предъявляет требования к реализации. Для ускорения вычислений и оптимальной работы предпочтительно предварительно вычислять необходимые синусоидальные и косинусоидальные значения углов вращения на основной позиции, а затем использовать их в режиме ускоренной свертки с запросами и ключами. При этом важно корректно обрабатывать пропорцию частот, которая равна нулю – этот прием способствует уменьшению избыточной сложности и повышает стабильность обучения. В перспективе применение N-мерных ротационных позиционных эмбеддингов может существенно расширить возможности трансформеров для задач, связанных с обработкой сложных структурированных данных — трехмерных объектов, временных рядов с несколькими координатами, мультимодальных данных и т. д.